一种新型量子秘密共享方案

　　论文《一种新型量子秘密共享方案》发表在《北京电子科技学院》，本文仅共展示，来自网络平台。

　　摘要：本文基于星型簇态的高度纠缠性和灵活拓扑结构设计了一种新型量子秘密共享方案，通过量子信道和经典信道的结合，确保秘密信息在多方之间的安全传输，实现了经典秘密和量子秘密的安全共享。在经典秘密共享方面，方案通过Pauli-Z和Pauli-X测量生成子密钥，并通过异或操作生成加密密钥，确保只有所有代理合作才能恢复明文。在量子秘密共享方面，方案通过Bell基测量和局域量子操作，确保只有指定的代理能够恢复出原始的量子态。该方案的创新之处在于支持多比特的扩展共享，进一步提高了系统的可扩展性;同时，该方案可在量子信道中根据实际应用需求对网络中的用户端实施增加或删除操作，增强了方案的灵活性。分析表明，该方案能够有效抵御非法窃听者的拦截-重发攻击和纠缠-测量攻击，同时也能避免合法参与者的共谋攻击。

　　关键词：量子密码;秘密共享;量子纠缠;局域操作

　　中图分类号：TN918

　　文献标识码：A

　　文章编号：1672-464X(2025)2-21-30

　　1 引言

　　量子保密通信起源于20世纪60年代，Wiesner提出了通过量子物理实现不可伪造量子货币的概念，并在文献[1]中详细描述了利用偏振光子存储和传输信息的方式。受到Wiesner的启发，Bennett和Brassard[2]发现，通信双方可使用适当的偏振光子在不安全的信道上生成一个加密密钥，这也正是如今广为人知的Bennett-Brassard1984(BB84)量子密钥分发(Quantum Key Distribution, QKD)协议，标志着量子密码学的开始。此后，诸多量子保密通信协议问世，这些协议大致可以分为四个主要分支：量子密钥分发协议[3]、量子隐形传态(Quantum Teleportation, QT)协议[4]、量子秘密共享(Quantum Secret Sharing, QSS)协议[5]和量子安全直接通信(Quantum Secure Direct Communication, QSDC)协议[6]。量子保密通信的安全性基于量子力学定律，而非基于数学难题，因此，其优势在于：即使出现具有无限算力的窃听者Eve，也能保证通信系统的安全。量子保密通信另一重要优势在于可以与一次一密(One-Time Pad, OTP)[7]相结合，充分利用一次一密的“只要密钥是随机均匀、不被重用的，密文信息就不会泄露”的特点，实现即使窃听者Eve截获密文，也无法在没有密钥的情况下恢复出明文，从而为通信提供理论上的无条件安全。

　　1999年，Hillery等人[5]提出了最初的量子秘密共享方案，利用三量子和四量子纠缠的Greenberger-Horner-Zeilinger(GHZ)态，在所有参与者共同协作的情况下，在多个参与者之间共享一个随机比特。2004年，Xiao等人[8]扩展了Hillery等人提出的方案框架，通过非对称选择测量基以适应多方参与的场景。此后，诸多一对多量子秘密共享协议被提出[9-18]。2005年，Yan和Gao提出了一种开创性的利用单量子的多对多量子秘密共享协议[9]。2008年，Yang和Wen提出了一种针对单量子序列的量子秘密共享方案[10]，适用于两个参与人数可能不同的小组协作重构秘密的情况。2010年，Shi等人提出了一种基于Bell态的多对多量子秘密共享协议[11]，参与者通过Bell态测量推导共享密钥。2011年，Yang等人提出了允许调整参与者的动态量子秘密共享协议[12]，但该协议是资源密集型的。此后也涌现了若干具有不同功能特点的支持网络动态调整参与者的量子秘密共享协议[13-18]。

　　2023年，Yang等人借助于通过对链式簇态进行局域Pauli-X测量和局域Pauli-Z测量得到的一种多量子纠缠态——星型簇态[19]，提出了一种基于具有分级结构的星型簇态的动态分级量子秘密共享协议[18]用以共享彼此正交的量子秘密，可实现参与者的增加和删除、升级和降级，并能根据参与者的等级分配不同的份额信息。受此启发，在现有量子秘密共享的研究基础上，本文基于星型簇态的拓扑结构，利用其高度纠缠特性设计了一种新型量子秘密共享协议，给出了利用该方案共享经典秘密与量子秘密的具体流程，完成了方案的安全性分析与秘密共享效率计算。

　　基金项目：中央高校基本科研业务费资金资助(课题编号:3282024026);supported by “the Fundamental Research Funds for the Central Universities”(Grant Number:3282024026);北京电子科技学院硕士精品示范课程项目“量子密码”。

　　作者简介：周睿雅(2003-)，女，本科生在读，研究方向为密码与信息安全;郑润芃(2003-)，女，本科生在读，研究方向为密码与信息安全;孙莹(1982-)，女，副教授，研究方向为量子保密通信协议与现代密码理论;刘昂(1988-)，男，工程师，研究方向为量子安全多方计算与区块链安全。

　　2 方案设计

　　本文采用如式(1)所示的由一个中心量子比特A和n个相邻的两量子比特臂(B_{i}A_{i}(i=1,2,cdots,n))构成的星型簇态[19](|C_{n}>_{AB_{1}A_{1}cdots B_{n}A_{n}})构建安全的量子信道完成秘密共享。

　　2.1 注册阶段

　　2.1.1 信道建立

　　Alice制备N个((2n+1))量子星型簇态分别记为

　　其中，(i=1,2,cdots,N)。

　　Alice保留量子(A_{i},A_{i1},cdots,A_{in})，将量子(B_{i1},cdots,B_{in}(i=1,2,cdots,N))分别发送给(Bob_{1},cdots,Bob_{n})。

　　2.1.2 窃听检测

　　对上述基于星型簇态制备的量子信道进行窃听检测，无需引入任何新的量子资源。具体步骤如下：

　　Alice对所持有的量子(A_{i})随机进行Pauli-Z或Pauli-X测量，(i=1,2,cdots,n)，Alice依序记录上述n次量子测量结果。(Bob_{1},cdots,Bob_{n})也分别对所持有的量子(B_{1},cdots,B_{n})随机进行Pauli-Z或Pauli-X测量，(Bob_{1},cdots,Bob_{n})依序分别记录上述n次量子测量结果，并通过经典信道通知Alice自己选用的测量基和测量结果。

　　Alice依序比较自己选用的测量基和收到的(Bob_{1},cdots,Bob_{n})的测量基，若测量基选用情况符合表1，则说明该位选用了正确的测量基，保留该位的测量结果。

　　Alice核对比较自己的测量结果和保留的(Bob_{1},cdots,Bob_{n})的测量结果，若(Bob_{1},cdots,Bob_{n})的测量结果均正确或误码率未超过信道噪声可能造成的错误阈值，可视作此量子信道没有遭到Eve窃听。到此，基于星型簇态的量子信道建立完成。

　　注意，进行上述窃听检测的量子态数量应不少于和(Bob_{1},cdots,Bob_{n})之间共享的全部星型簇态数量的50%，确保用于窃听检测的样本足够大，统计结果可靠。若所有完成窃听检测的信道错误率均未超过阈值时，则认为信道中星型簇态被安全共享，可以继续执行协议的其他步骤。

　　2.1.3 用户管理

　　2.1.3.1 增加用户

　　假设想要增加(Bob_{n+1})到(Bob_{1},cdots,Bob_{n})中，因此要在已安全共享的星型簇态(|C_{n}>_{AB_{1}A_{1}cdots B_{n}A_{n}})的基础上，制备一个三量子线性簇态

　　Alice对所持有的量子对((A,A'))进行C-Z门操作，其中A为控制量子比特、(A')为目标量子比特，得到

　　Alice接着对量子(A')进行局域测量，测量后，信道内剩余量子坍缩状态用(|C_{n+1}>_{AB_{1}A_{1}cdots B_{n+1}A_{n+1}})表示。

　　Alice对所持有的量子(A_{n+1})进行相应的量子局域操作后，整个系统状态可以由下式描述：

　　2.1.3.2 删除用户

　　假设想要从(Bob_{1},cdots,Bob_{n})中删除(Bob_{j})，(jin{1,2,cdots,n})，因此要在已安全共享的星型簇态(|C_{n}>_{AB_{1}A_{1}cdots B_{n}A_{n}})的基础上对量子(A_{j})进行局域Pauli-Y测量，测量后，信道内剩余量子坍缩状态用(|C_{n-1}>_{AB_{1}A_{1}cdots B_{j-1}A_{j-1}B_{j+1}A_{j+1}cdots B_{n}A_{n}})表示。

　　量子对((A_{j},B_{j}))从量子态(|C_{n}>_{AB_{1}A_{1}cdots B_{n}A_{n}})中解纠缠，根据图态局域Pauli测量规则，整个系统演化为如下状态

　　2.2 经典比特的秘密共享方案

　　2.2.1 单比特方案设计

　　2.2.1.1 分发阶段

　　假设要分享比特消息M给(Bob_{1},cdots,Bob_{n})。Alice对持有的量子A和(A_{i}(i=1,2,cdots,n))均进行Pauli-Z测量或随机选择一个进行Pauli-Z测量、另一个进行Pauli-X测量，并依据表2通过经典信道通知(Bob_{i})应选用的测量基。(Bob_{i})对所持有的量子(B_{i})进行测量后用测量结果生成(Bob_{i})的子密钥(k_{i})，若测量出的量子态为|0>或|+>，记(k_{i}=0);若测量出的量子态为|1>或|-，记(k_{i}=1)。

　　2.2.1.2 重构阶段

　　对于A、(A_{i})、(B_{i}(i=1,2,cdots,n))三个量子，随机对其中两个进行Pauli-Z测量、另一个进行Pauli-X测量，测量出的量子态唯一确定。因此，Alice只要测量了A、(A_{i})这两个量子就能知道量子(B_{i})的量子态并获知(Bob_{i})的子密钥(k_{i})。

　　Alice对(Bob_{1},cdots,Bob_{n})的子密钥(k_{1},cdots,k_{n})进行异或操作得到加密密钥(K_{C}=k_{1}opluscdotsoplus k_{n})。加密明文M，得到密文(C=K_{C}oplus M=k_{1}opluscdotsoplus k_{n}oplus M)。假设选定(Bob_{1})为最终恢复出明文的参与者，Alice通过经典信道将密文C分享给(Bob_{1})。

　　(Bob_{2},cdots,Bob_{n})对子密钥(k_{2},cdots,k_{n})进行异或操作，将计算结果通知(Bob_{1})，(Bob_{1})将子密钥(k_{1})和上述计算结果进行异或操作得到解密密钥(K_{M}=k_{1}opluscdotsoplus k_{n})。解密密文C，得到明文(M'=K_{M}oplus C=k_{1}opluscdotsoplus k_{n}oplus k_{1}opluscdotsoplus k_{n}oplus M=M)，即得到Alice想要分享的1比特消息。

　　2.2.2 多比特方案设计

　　2.2.2.1 分发阶段

　　假设要分享m比特消息M。对m个星型簇态均做上述量子测量操作，得到n个m比特01串，即为生成的(Bob_{1},cdots,Bob_{n})的子密钥串。Alice能够知道所有量子(B_{i})的测量结果并获知(Bob_{1},cdots,Bob_{n})的子密钥串(k_{1}',cdots,k_{n}')。

　　2.2.2.2 重构阶段

　　Alice对(Bob_{1},cdots,Bob_{n})的子密钥串(k_{1}',cdots,k_{n}')进行异或操作得到加密密钥(K_{C}'=k_{1}'opluscdotsoplus k_{n}')。加密明文M，得到密文(C=K_{C}'oplus M=k_{1}'opluscdotsoplus k_{n}'oplus M)。假设选定(Bob_{1})为最终恢复出明文的参与者，Alice通过经典信道将密文C分享给(Bob_{1})。

　　(Bob_{2},cdots,Bob_{n})对子密钥(k_{2}',cdots,k_{n}')进行异或操作，将计算结果通知(Bob_{1})，(Bob_{1})将子密钥(k_{1}')和上述计算结果进行异或操作得到解密密钥(K_{M}'=k_{1}'opluscdotsoplus k_{n}')。解密密文C，得到明文(M'=K_{M}'oplus C=k_{1}'opluscdotsoplus k_{n}'oplus k_{1}'opluscdotsoplus k_{n}'oplus M=M)，即得到想要分享的m比特消息。

　　2.3 量子比特的秘密共享方案

　　2.3.1 单量子比特方案设计

　　2.3.1.1 分发阶段

　　假设Alice要分享1量子比特的秘密量子态(|varphi>_{a}=alpha|0>+eta|1>)给(Bob_{1},cdots,Bob_{n})，其中(|alpha|^{2}+|eta|^{2}=1)。

　　Alice首先通过经典信道通知(Bob_{i}(i=1,2,cdots,n))对所持有的星型簇态中的量子(B_{i})进行H门操作，定义该操作(U=I_{a}otimes I_{A}otimes H_{B_{1}}otimes I_{A_{1}}otimescdotsotimes H_{B_{n}}otimes I_{A_{n}})，得到

　　假设选定(Bob_{1})为最终恢复出量子态的参与者，对所持有的量子对((a,A_{j}))进行C-NOT门操作，其中a为控制量子比特，(A_{j})为目标量子比特，(j=2,3,cdots,n)，得到

　　Alice对量子((a,A_{1}))进行Bell基测量，测量后，系统内剩余量子坍缩状态(|psi'''>_{AB_{1}B_{2}A_{2}cdots B_{n}A_{n}})如表3所示。接着对量子(A_{j}(j=2,3,cdots,n))进行测量，系统内剩余量子坍缩状态用(|psi''''>_{AB_{1}cdots B_{n}})表示，记录和妥善保存上述n次量子测量结果。

　　2.3.1.2 重构阶段

　　若允许(Bob_{1})在此之后恢复出量子态，即Alice想要继续本秘密共享协议，其需要通过经典信道将上述n次量子测量结果分享给(Bob_{1},cdots,Bob_{n})，并对量子A进行测量，系统内剩余量子坍缩状态用(|psi'''''>_{B_{1}cdots B_{n}})表示。

　　(Bob_{2},cdots,Bob_{n})分别对持有的量子(B_{2},cdots,B_{n})进行Pauli-X测量，并通过经典信道将量子测量结果发送给(Bob_{1})。

　　(Bob_{1})对收到的量子测量结果进行分类统计，当收到的测量结果为|-〉的数量是奇数时，(Bob_{1})所持有的量子(B_{1})塌缩状态为(|psi'''''>_{B_{1}}=alpha|0>-eta|1>);当收到的测量结果为|-〉的数量是偶数时，(Bob_{1})所持有的量子(B_{1})塌缩状态为(|psi'''''>_{B_{1}}=alpha|0>+eta|1>)。

　　(Bob_{1})依据收到的量子测量结果对量子(B_{1})的量子态(|psi'''''>_{B_{1}})进行相应的幺正变换，即恢复出Alice想要分享的秘密量子态(|varphi>)。

　　2.3.2 多量子比特方案设计

　　2.3.2.1 分发阶段

　　假设要分享一个m量子比特的秘密量子态(|varphi'>_{a_{1}a_{2}cdots a_{m}}=alpha|0cdots0>+eta|1cdots1>)，其中(|alpha|^{2}+|eta|^{2}=1)。系统初态为

　　Alice首先通过经典信道通知(Bob_{i}(i=1,2,cdots,n))对所持有的量子(B_{i})进行H门操作，定义该操作(U_{1}=I_{a_{1}}otimes I_{a_{2}}otimescdotsotimes I_{a_{m}}otimes I_{A}otimes H_{B_{1}}otimes I_{A_{1}}otimescdotsotimes H_{B_{n}}otimes I_{A_{n}})，整个量子系统转化为

　　a) 若(m < n)

　　假设选定(Bob_{1})为最终恢复出量子态的参与者，对所持有的量子对((a_{1},A_{j}))进行CNOT门操作，其中(a_{1})为控制量子比特，(A_{j})为目标量子比特，(j=m+1,m+2,cdots,n)，得到

　　Alice对量子((a_{k},A_{k}))进行m次Bell基测量，(k=1,2,cdots,m)，测量后系统内剩余量子坍缩状态用(|psi'''>_{AB_{1}B_{2}cdots B_{m+1}A_{m+1}cdots B_{n}A_{n}})表示。Alice接着对量子(A_{j}(j=m+1,m+2,cdots,n))进行(n - m)次测量，系统内剩余量子坍缩状态用(|psi''''>_{AB_{1}cdots B_{n}})表示，记录和妥善保存上述n次量子测量结果。

　　b) 若(m = n)

　　假设选定(Bob_{1})为最终恢复出量子态的参与者，对量子((a_{k},A_{k}))进行n次Bell基测量，(k=1,2,cdots,n)，测量后系统内剩余量子坍缩状态用(|psi'''>_{AB_{1}cdots B_{n}})表示，记录和妥善保存上述n次量子测量结果。

　　c) 若(m > n)

　　假设选定(Bob_{1})为最终恢复出量子态的参与者，对量子((a_{k},A_{k}))进行n次Bell基测量，(k=1,2,cdots,n)，测量后系统内剩余量子坍缩状态用(|psi'''>_{a_{n+1}a_{n+2}cdots a_{m}AB_{1}B_{2}cdots B_{n}})表示。Alice接着对量子(a_{j}(j=n+1,n+2,cdots,m))进行(m - n)次Pauli-Z测量，系统内剩余量子坍缩状态用(|psi''''>_{AB_{1}cdots B_{n}})表示，记录和妥善保存上述n次量子测量结果。

　　2.3.2.2 重构阶段

　　若允许(Bob_{1})在此之后恢复出量子态，即Alice想要继续本秘密共享协议，其需要通过经典信道将上述n次量子测量结果分享给(Bob_{1},cdots,Bob_{n})，并对量子A进行测量，系统内剩余量子坍缩状态用(|psi'''''>_{B_{1}cdots B_{n}})表示。

　　(Bob_{2},cdots,Bob_{n})分别对持有的量子(B_{2},cdots,B_{n})进行Pauli-X测量，并通过经典信道将量子测量结果发送给(Bob_{1})。(Bob_{1})依据收到的量子测量结果对量子(B_{1})的量子态(|psi'''''>_{B_{1}})进行相应的幺正变换，并对(m - 1)个初态为|0>的量子进行(m - 1)次CNOT门操作，其中(B_{1})为控制量子比特、|0>为目标量子比特，即恢复出Alice想要分享的秘密量子态(|varphi'>_{a_{1}a_{2}cdots a_{m}})。

　　3 方案分析

　　3.1 安全性分析

　　3.1.1 非法窃听者攻击

　　a) 拦截-重发攻击

　　假设存在窃听者Eve，在Alice建立信道发送量子的过程中，拦截获取一个量子，并准备一个假冒量子发送给(Bob_{1},cdots,Bob_{n})中任意的参与者。在窃听检测过程中，若参与者选择使用的测量基与Alice使用的测量基相同，则该测量无效，测量结果被丢弃，Eve的拦截-重发操作没有引入任何错误;若参与者使用的测量基与Alice使用的测量基不同，则该测量有效，Alice根据测量结果判断量子信道是否遭到窃听，Eve的拦截-重发操作会以50%的概率引入错误。若Eve拦截重发t个量子，则引入错误的总概率可表示为(1 - (frac{3}{4})^{t})。显然当(t o infty)时，此概率值(P = 1 - (frac{3}{4})^{t})趋近于100%。因此，若窃听者Eve采用拦截-重发攻击，在检测样本足够大的情况下一定会被检测到。

　　b) 纠缠-测量攻击

　　假设存在窃听者Eve，在Alice建立信道发送量子的过程中，拦截获取一个发送给某个参与者的量子B，并对该量子进行联合幺正变换，将其与一个辅助量子(|varepsilon>)纠缠，定义该变换为

　　其中，依据量子态的归一性，(<varepsilon_{1}|varepsilon_{1}> + <varepsilon_{2}|varepsilon_{2}> = 1)，(<varepsilon_{3}|varepsilon_{3}> + <varepsilon_{4}|varepsilon_{4}> = 1);依据量子态的正交性，(<varepsilon_{1}|varepsilon_{2}> = <varepsilon_{3}|varepsilon_{4}> = 0);依据量子跨组态的正交性，(<varepsilon_{1}|varepsilon_{3}> = <varepsilon_{2}|varepsilon_{4}> = 0)。Eve测量辅助量子(|varepsilon>)，量子B保持原状态的概率：

　　由于量子B和辅助量子(|varepsilon>)处于纠缠态，(<varepsilon_{3}|varepsilon_{2}> eq 0)，(P_{nd}(|+>) < 1)，(P_{nd}(|->) < 1)，因此，若窃听者Eve采用纠缠-测量攻击，则同样能够被检测到。

　　3.1.2 合法参与者攻击

　　a) 窃听攻击

　　假设存在参与者(Bob_{t})是不诚实的参与者，想要窃取秘密信息。若(Bob_{t})在建立信道发送量子的过程中，拦截获取发送给其它参与者的量子，则攻击情况同非法窃听者Eve的拦截-重发攻击，能够被检测。若(Bob_{t})在(Bob_{1},cdots,Bob_{n})重构秘密的过程中，试图获知其它参与者对持有的量子B进行单量子测量的结果，但由于测量结果为|0>和|1>、|+>和|-〉是随机的，(Bob_{t})无法依据自己的测量结果推断其它参与者的测量结果，因此，既无法得到Alice想要分享的经典比特消息，也无法恢复出Alice想要分享的未知量子态(|varphi>)。综上所述，合法参与者的窃听攻击无法成功。

　　b) 共谋攻击

　　假设存在t个参与者，(t < n)，在(Bob_{1},cdots,Bob_{n})重构秘密的过程中实施共谋攻击。若这t个不诚实参与者企图共谋重构经典比特秘密，解密密钥(K_{M}=k_{1}opluscdotsoplus k_{n})。但由于Alice的测量结果是随机的，且每个参与者的两量子比特臂相互独立，因此任何t个参与者都不能共谋获知所有的子密钥k，无法恢复出解密密钥(K_{M})，无法得到Alice想要分享的经典比特消息;若t个不诚实的Bob共谋重构量子比特秘密，需要依据收到的量子测量结果对量子态(|psi'''>_{B_{1}})进行幺正变换，由于Alice的测量结果是随机的，且每个参与者的两量子比特臂相互独立，因此，任何t个参与者都不能共谋获知由除最终恢复出量子态之外的参与者持有的量子B的测量结果，无法分类统计测量结果为|-〉的数量是奇数还是偶数，也就无法确定地恢复出Alice想要分享的未知量子态(|varphi>)。综上所述，合法参与者的共谋攻击无法成功。

　　3.2 效率分析

　　3.2.1 共享经典比特

　　经典比特的秘密共享方案由(2n + 1)个量子构成的星型簇态实现。每共享1比特经典秘密，需要进行(2n + 1)次Pauli测量，同时辅以(2n + 1)比特经典通信。

　　定义经典比特共享效率

　　3.2.2 共享量子比特

　　量子比特的秘密共享方案由(2n + 1)个量子构成的星型簇态实现。每共享1比特量子秘密，需要进行1次Bell基测量、(n)次Pauli-Z测量、(n - 1)次Pauli-X测量、(n)次H门操作、(n - 1)次C-NOT门操作和1次单量子幺正变换，同时辅以(2n + 1)比特经典通信。

　　类似地，定义量子比特共享效率

　　当共享多量子比特时，若(m < n)，需要进行(m)次Bell基测量、(n - m + 1)次Pauli-Z测量、(n - 1)次Pauli-X测量、(n)次H门操作、(n - m)次C-NOT门操作和1次单量子幺正变换，辅以(2n + m)比特经典通信，共享效率可表示为

　　若(m > n)，需要进行(n)次Bell基测量、(m - n + 1)次Pauli-Z测量、(n - 1)次Pauli-X测量、(n)次H门操作和1次单量子幺正变换，辅以(2n + m)比特经典通信，共享效率可表示为

　　3.3 对比研究

　　为了更好地说明本文所提方案的优势，下面选取了两个相关的协议进行比较(如表4所示)。其中文献[14]选用了最典型的双量子最大纠缠态Bell态和常见的环形拓扑结构，与本文方案在协议执行过程中均采用了Bell基测量;文献[18]与本文选用了相同的簇态与网络拓扑结构。以上两个方案与本文方案同样具备动态操作能力和高可扩展性，均具有典型的意义。

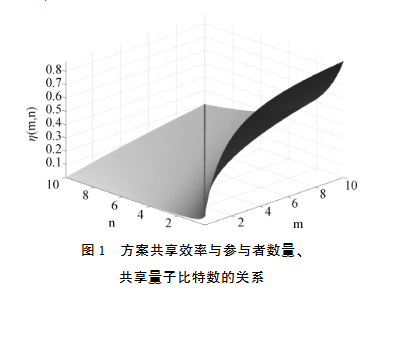
　　本文提出的秘密共享方案中关于量子秘密的共享效率如图1所示。从图中可以看出，当固定共享量子比特数m时，共享效率η与参与者数量n负相关，随着n增大，共享效率η逐渐减小;反之，当固定参与者数量n时，共享效率η与共享比特数m正相关，m增大，共享效率η随之增大，但整体上参与者数量n对于方案共享效率η的影响相对更大。

　　(图1 方案共享效率与参与者数量、共享量子比特数的关系)

　　4 结论

　　本文结合量子信道与经典信道，基于星型簇态的纠缠特性，提出了一种新型量子秘密共享方案，通过协议构建的量子信道实现了经典秘密和量子秘密的安全多方共享，分别描述了单比特秘密共享和多比特秘密共享的过程，展示了方案在复杂量子系统中的高可扩展性;同时，方案充分利用星型簇态具有良好拓扑结构的特点，允许在共享网络中动态地进行用户增加或删除操作，能够适应不同的应用场景，具有较强的实用性与灵活性。

　　通过分析可知，本方案具有良好的安全性，能够同时抵御来自非法窃听者和合法参与者带来的多种攻击;在具备高可操作性的基础上，还具有相对较高的通信效率。

　　参考文献

　　[1] Wiesner S. Conjugate coding[J]. ACM SIGACT News, 1983(15), 1:78-88.

　　[2] Bennett C H, Bessette F, Brassard G, Salvail L, Smolin J. Experimental quantum cryptography[J]. Cryptology, 1992(5), 1:3-28.

　　[3] Bennett C H, Brassard G. Quantum cryptography: public key distribution and coin tossing[C]. International Conference on Computer System and Signal Processing, IEEE, 1984.

　　[4] Bennett C H, Brassard G, Crepeau C, Jozsa R, Peres A, Wootters W K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels[J]. Physical Review Letters, 1993(70), 13:1895-1899.

　　[5] Hillery M, Buzek V, Berthiaume A. Quantum secret sharing[J]. Physical Review A, 1999, 59:1829-1834.

　　[6] Long G L, Liu X S. Theoretically efficient high-capacity quantum-key-distribution scheme[J]. Physical Review A, 2002, 65:032302.

　　[7] Armanuzzaman M, Alam K M R, Hassan M M, Morimoto Y. A secure and efficient data transmission technique using quantum key distribution[C]. International Conference on Networking, Systems and Security, IEEE, 2017.

　　[8] Xiao L, Long G L, Deng F G, Pan J W. Efficient multiparty quantum-secret-sharing schemes[J]. Physical Review A, 2004, 69:052307.

　　[9] Yan F L, Gao T. Quantum secret sharing between multiparty and multiparty without entanglement[J]. Physical Review A, 2005, 72:012304.

　　[10] Liao Q, Liu H, Zhu L, Guo Y. Quantum secret sharing using discretely modulated coherent states[J]. Physical Review A, 2021, 103:032410.

　　[11] Shi R H, Huang L S, Yang W, Zhong H. Quantum secret sharing between multiparty and multiparty with Bell states and Bell measurements[J]. SCIENCE CHINA Physics, Mechanics and Astronomy, 2010(53):2238-2244.

　　[12] Yang Y G, Wang Y, Chai H P, Teng Y W, Zhang H. Member expansion in quantum (t, n) threshold secret sharing schemes[J]. Optics Communications, 2011, 284:3479-3482.

　　[13] Jia H Y, Wen Q Y, Gao F, Qin S J, Guo F Z. Dynamic quantum secret sharing[J]. Physics Letters A, 2012, 376:1035-1041.

　　[14] Hsu J L, Chong S K, Hwang T, Tsai C W. Dynamic quantum secret sharing[J]. Quantum Information Processing, 2013, 12:331-344.

　　[15] Sun Y, Xu S W, Chen X B, et al. Expandable quantum secret sharing network[J]. Quantum Information Processing, 2013, 12 (8):2877-2888.

　　[16] Liao C H, Yang C W, Hwang T. Dynamic quantum secret sharing protocol based on GHZ state[J]. Quantum Information Processing, 2014, 13:1907-1916.

　　[17] Qin H, Tang W K, Tso R. Multiparty to multiparty quantum secret sharing[J]. Physics Letters B, 2018, 32:1850350.

　　[18] 杨宇光, 卢嘉煜. 一种基于星型簇态的动态的分级的量子秘密共享协议[J]. 信息网络安全, 2023, 23(06):34-42.

　　[19] Chen Q, Cheng J, Wang K L, Du J. Efficient construction of two-dimensional cluster states with probabilistic quantum gates[J]. Physical Review A, 2006, 73:012303.