基于RF-Light GBM的分组密码算法识别方案

　　论文《基于RF-Light GBM的分组密码算法识别方案》发表在《北京电子科技学院学报》，本文仅共展示，来自网络平台。

　　摘要密码算法的识别在密码分析领域中具有重要意义。目前主流分组密码算法识别方案中，密文特征提取普遍基于随机性检测标准。为解决短样本识别需求以及进一步提高识别准确率，本研究提出了一种基于RF-LightGBM的分组密码体制识别方案。首先通过GM/T0005-2021随机性检测标准提取密文特征，其次利用随机森林算法对高维的数据进行重要性排序和筛选，然后利用特征向量训练LightGBM算法模型构建密码算法识别分类器进行识别。实现了短样本环境下高效识别未知密文的识别需求。在两两识别实验中，与现有研究相比本方案准确率整体提升约12%;多分类实验显示准确率均在73%以上，验证了本方案在分组密码算法识别中的有效性和优势，为未来在更复杂的加密模式下进行密码算法识别提供了参考。

　　关键词：分组密码;机器学习;随机性检测;密码算法识别;LightGBM

　　0 引言

　　随着信息安全需求的不断增长，密码学在保护数据机密性和完整性方面发挥着至关重要的作用。作为对称加密算法的基础之一，分组密码算法被广泛应用于各种加密系统中，如数据存储、网络通信和金融交易等领域。分组密码算法的核心目标是通过对固定长度数据块的加密，实现数据的保密性。然而，随着密码学研究的深入，密文分析技术的不断发展，密码算法的识别问题逐渐成为学术界和工业界的研究热点[1]。通过分析密文的特征信息，识别出加密所使用的算法，可以有效地评估密码系统的安全性，并对潜在的攻击风险进行预测[2]。

　　分组密码算法的识别主要是通过分析加密后的密文，推测出其所采用的具体加密算法[3]。随着加密算法的不断进化，密文的特征往往变得更加复杂和难以直接辨识。近年来，机器学习方法被逐渐引入到密码算法识别领域，尤其是集成学习和深度学习方法的应用，显著提升了识别的准确性和效率。具体来说，基于机器学习的密码算法识别系统首先通过从密文中提取特征，构建特征向量，然后利用分类算法进行训练和识别。

　　目前，主流分组密码识别方案中的密文特征提取主要基于随机性检测标准，其中，主要为NIST SP800-22随机性检测标准[4]和GM/T0005-2021随机性检测规范[5]。GM/T0005-2021随机性检测规范是国家密码管理局于2021年发布的一项重要标准，是在GM/T0005-2012随机性检测规范的基础上进行了修订和扩展，适用范围从原先的“适用于对随机数发生器产生的二元序列的随机性检测”扩展为“适用于对二元序列的随机性检测”，进一步提升了其普适性和实用性。由此本文选择GM/T0005-2021标准的15种检测方法作为提取特征向量方法。

　　如今，机器学习方法逐渐在密码识别领域中被广泛应用[6]，此方法有着坚实的理论基础和丰富的实践经验，并且在设计过程中表现出相对的简单性和稳定性，能够有效处理数据之间复杂的关系。这使得基于机器学习的密码识别方案在效率和准确性上均取得了显著的优势。所以本文结合了机器学习算法和GM/T0005-2021标准提出了基于RF-LightGBM的分组密码算法识别方案，旨在进一步探索短样本环境下对未知密文进行高效快速识别，为密码算法设计和安全性评估提供一定的参考。

　　基金项目：中央高校基本科研业务费专项资金资助项目(3282024046)。

　　作者简介：董秀则(1976-)，男，山东莒县人，副教授，研究方向为信息安全与密码工程;杨鸿刚(1999-)，男，河北沧州人，硕士研究生，研究方向为网络空间安全;胡一凡(2001-)，男，安徽合肥人，硕士研究生，研究方向通信工程;于庚辰(2000-)，男，山东临沂人，硕士研究生，主要研究方向网络空间安全。

　　1 相关工作

　　2018年，黄良韬等人[7]对已有密码算法分类研究进行了总结，并提出了一个密码算法识别系统，该系统利用随机森林算法对古典密码、流密码、分组密码和公钥密码进行了层次化识别。2019年，赵志诚等人[8]综合使用随机性测试、比特熵和不定长文本向量等方法，设计了密文特征，并对Grain-128密码算法与其他11种对称密码算法进行了逐对区分。同年，赵志诚等人[9]基于NIST随机性测试标准，提出了一个基于随机森林的密码体制识别方案，该方案能有效区分明密文及不同模式的分组密码密文，还能准确识别AES、DES、3DES等六种密码体制。

　　2021年，纪文桃等人[10]和曹莉茹[11]分别实现了对商密SM4算法与其他分组密码算法的逐对识别以及对八种密码算法进行了分类。二者方案都通过随机性测试选择密文特征，后者通过BP神经网络、卷积神经网络和循环神经网络等深度学习方法。

　　2022年，刘节威等人[12]实现了对商密SM4算法与其他算法的识别。通过对商用分组密码算法进行识别研究，提出了一种结合自动编码器和卷积神经网络的识别方案。同年，夏锐琪等人[13]提出了一种基于机器学习和特征工程的加密模式识别方法，采用5种加密方式进行识别。

　　2023年，袁科等人[14]以分组密码算法为研究对象，提出一种混合随机森林和逻辑回归模型的分组密码算法辨识方案，基于NIST随机性特征提取方法，选取AES、3DES、Blowfish、CAST和RC2五个分组密码作为研究对象，开展密文分类任务。同年，夏锐琪等人[15]将游程分布指标、特征分布函数和KL散度等概念融入研究中，探究Feistel和SPN结构的不同，构建了机器学习模型，对十二种分组密码算法进行识别。

　　2024年，张运理等人[16]采用随机数检测规范中的检测项对密文进行检测得到P_Value和Q_Value，并将其作为密文特征项，基于集成学习模型构建了识别模型，实现了唯密文场景下的分组密码算法识别技术。

　　2 基本理论

　　2.1 机器学习识别原理

　　在探讨密码算法的多样性时，必须认识到不同算法在核心设计理念、组件架构、操作机制以及密钥管理方式上的本质区别。这种差异，加之明文数据类型的多样性，可能会影响加密后密文的空间分布特征[17]。因此，对于密文识别的核心在于精确捕捉这些密文数据之间的细微差异，以实现密码算法类型的精准区分[18]。

　　目前，密码算法识别的研究主要采用分类思想，构建的完整识别系统分为两个主要部分。首先，对密文文件进行提取密文特征，然后汇总生成特征向量。其次，选择分类算法，输入特征向量进行训练，以完成分类任务。文献[9]给出了完整的密码体制识别方案的定义是(Gamma=(M, J, h^{J}))。

　　密码算法集合(M={m_1, m_2, cdots, m_n})，其中n为密码算法的个数。J代表当前密码体制识别的策略，(h^{J})是密文识别结果的评价指标，指的是在当前密码识别条件下，识别方案可正确识别密码体制的概率或准确率。在公式(Gamma=(M, J, h^{J}))中，核心部分是密码体制识别方案J，一般的J表示为三元组结构如式(J=(oper, fea, CA))。

　　三元组中的oper代表识别方案的具体工作流程，fea为从密文中提取出的特征，CA是识别过程中具体用到的识别算法。

　　2.2 梯度提升的基本原理

　　梯度提升(Gradient Boosting)的基本原理是通过构建一系列的弱学习器(通常是决策树)，每个新的学习器都试图修正前一个学习器的错误，从而逐步提高整体模型的性能[19]。

　　梯度提升模型表示为：

　　[F(x)=sum_{m=1}^{K} eta_{m} h_{m}(x)]

　　其中，(h_m(x))是第m棵决策树，(eta_m)是其对应的权重。

　　初始化模型：

　　[F_{0}(x)=arg min _{eta} sum_{i=1}^{N} Lleft(y_{i}, eta ight)]

　　其中，(L(x, y))为损失函数，意为找出一个变量(或一组变量)，使得一个给定函数在这些变量取值时达到最小值;(eta)是第i个样本通过当前决策树模型的预测值，(y_i)是第i个样本的真实值。

　　计算当前模型的残差：

　　[r_{i, m}=-left[frac{partial Lleft(y_{i}, Fleft(x_{i} ight) ight)}{partial Fleft(x_{i} ight)} ight]_{F(x)=F_{m-1}(x)}]

　　拟合一棵新树(h_m(x))来预测残差。

　　更新模型：

　　[F_{m}(x)=F_{m-1}(x)+eta_{m} h_{m}(x)]

　　其中，(eta_m)是步长(学习率)。

　　2.3 P_value值

　　P_value值[11]是指在期望(理论)分布中观察到的统计量与在具体实验中所得到的统计量相同或更大的概率。在假设检验的框架内，它反映了在零假设为真的条件下，获得当前或更极端结果的可能性。当计算出的P_value值高于预设的显著性水平(alpha)时，我们认为零假设是可以接受的;反之，则应拒绝零假设。对于随机数序列检测，P_value表明序列是否偏离了随机性假设。

　　Q_value值是一种校正后的显著性概率，用来衡量在多重假设检验中，将某一个假设判为显著(拒绝零假设)时，错误拒绝的概率(即假阳性概率)。

　　3 密码算法识别方案

　　3.1 方案总体框架

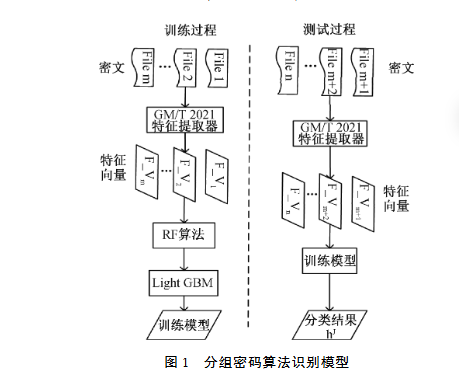
　　如图1所示，本识别方案包含训练阶段和测试阶段。先使用研究的密码算法对其明文进行加密得到对应的密文。在训练阶段，首先收集P种密码算法加密的组密文文件，每组包含n个文件，为了划分数据集，将每组n个文件划分10等份，其中每一份都作为一次验证的测试集，其余九份作为训练集。具体来说，整个过程将进行10次，每次选择不同的一份作为测试集，其余九份作为训练集，通过这种交叉验证的方法，可以全面利用每个密文数据。然后，通过GM/T0005-2021特征提取器对抽取的密文数据进行特征提取，密文输入进提取器会生成对应的P_value值作为特征向量，构成特征矩阵，每一行代表一个密文文件，每列代表一个提取的特征。再对每个特征向量标记与其密码体制类别相对应的标签，这些特征向量被整合在一起组成训练集。然后，采用随机森林算法对每个特征进行重要性评估，通过计算特征在决策树中的贡献度，能够判断出哪些特征对加密算法的识别最有帮助。基于这些评估结果，筛选出最具区分性的特征集。这些选定的特征集被输入到LightGBM分类器中，进行模型训练。LightGBM使用梯度提升决策树(GBDT)方法，高效地处理大规模数据，生成准确性和鲁棒性较高的分类模型。

　　在测试阶段，将剩余的特征向量作为测试集输入到已经训练好的LightGBM分类器中，进行分类测试，最终输出每个密文的加密算法类别，并通过准确率、召回率和F1值等指标评估分类效果。通过这一步骤，实现了对分组密码算法的识别，确保了本方案在识别不同密码算法加密的密文时具有高度的准确性和可靠性。

　　(图1 分组密码算法识别模型)

　　3.2 随机森林

　　随机森林是一种强大的集成学习方法，通过构建多个在不同数据子集上训练的决策树并结合它们的预测结果来提高模型性能和稳定性[20]。它利用随机抽样和随机特征选择来增加模型多样性、降低过拟合风险，并通过投票机制或平均值集成决策树的预测结果，适用于分类和回归任务，通常具有较高准确性。

　　本文结合过滤式和包裹式方法来筛选特征集，其中过滤式方法使用特征选择算法进行筛选，包裹式方法则通过评估模型性能变化来选择最佳特征集。随机森林算法在很大程度上克服了模型过拟合的问题，具有良好的泛化性能和较高的预测精度[21]。此外，它能够有效处理高维特征的数据，评估各个特征的重要性，并按重要性进行排序。

　　3.3 LightGBM分类器

　　LightGBM作为实现GBDT(Gradient Boosting Decision Tree)算法框架之一，支持高效率的并行训练，并且具有更快的训练速度、更低的内存消耗、更好的准确率，以及支持分布式可以快速处理海量数据等优点[22]。LightGBM在传统的GBDT算法上进行了直方图算法、GOSS、EFB、Leaf-wise树生长策略以及支持类别特征等优化措施[23]。由此本文将LightGBM模型引入到分组密码识别方案中，探讨研究利用未知密文识别分组密码加密结构的问题。

　　LightGBM使用直方图算法(Histogram)对特征值进行离散化，减少了特征分裂点的计算量[24]。传统的GBDT需要遍历所有特征值来找到最佳分裂点，而直方图算法通过将特征值划分为固定数量的区间(bins)，如在本方案中特征向量为0到1的浮点数，可以将其划分为5个区间，然后在直方图上找到最优的分裂点，通过计算每个区间的分裂增益，选择增益最大的区间进行分裂。通过减少计算分裂点的次数，显著降低了计算复杂度。

　　对于分割点的增益Gain可定义为式(5)：

　　[Gain =sum_{i=1}^{left} w_{i}+sum_{j=1}^{right} w_{j}-sum_{k=1}^{all} w_{k}]

　　其中，(sum_{i=1}^{left} w_{i})和(sum_{j=1}^{right} w_{j})分别代表左右子节点梯度统计量，(sum_{k=1}^{all} w_{k})代表初始节点的梯度统计量总和。

　　如图2所示，在Histogram算法之上，LightGBM进行进一步的优化，使用了带有深度限制的按叶子生长(leaf-wise)算法。该算法每次选择当前所有叶子节点中分裂增益最大的叶子进行分裂，能生成更深的树结构。这种策略可以更好地处理不平衡的数据分布，提高模型的精度[25]。在本分组密码算法识别方案中，Leaf-wise的生长方式使得每次分裂都能最大化信息增益，从而提升模型的学习能力和预测准确性，适用于本方案特征向量为浮点数这种高精度预测的场景。其中，选择信息增益最大的分裂，这个过程可以表示为式(6)：

　　[Gain =frac{1}{2}left[frac{G_{L}^{2}}{H_{L}+lambda}+frac{G_{R}^{2}}{H_{R}+lambda}-frac{left(G_{L}+G_{R} ight)^{2}}{H_{L}+H_{R}+lambda} ight]-gamma]

　　其中，(G_L)和(G_R)分别代表左子结点和右子节点的梯度和，(H_L)和(H_R)分别代表左子节点和右子节点的二阶导数和，(lambda)为正则化参数，(gamma)为叶子节点分裂的最小增益阈值。

　　LightGBM模型算法流程如图3所示，首先进行数据预处理，将连续特征离散化为k个桶，处理缺失值，将缺失值单独作为一个类别。然后进行初始化模型(F_0(x))。在迭代训练阶段，对每次迭代m：计算当前模型的残差;构建直方图，加速寻找最佳分割点;使用基于叶子的生长策略，选择当前损失最大的叶子节点进行分裂;最后更新模型(F_m(x))。训练完成后输出最终的预测模型(F_M(x))。

　　(图2 Leaf-wise树生长)

　　(图3 LightGBM模型算法流程)

　　4 实验设置及结果分析

　　4.1 数据集与参数设置

　　本文使用的明文数据来自AG News(AG's News Corpus)，将其随机切割出2000个32KB的文档，以二进制方式读取。为了加密这些文档，使用Crypto库对五种分组密码算法(DES、AES、3DES、Blowfish、RC2)进行了实现，通过OpenSSL库对IDEA、CAST、SM4这三种分组密码进行了实现。在所有的加密过程中，均为ECB工作模式，以确保加密的一致性，如表1所示。对同一密码算法在模型训练和测试的过程中，采用统一的密钥。为了提取这些密文文件的特性，编写了符合《GM/T0005-2021随机性检测规范》的Python代码作为特征提取器，对密文进行了特征提取，然后将这些特征向量进行汇总并打上算法对应标签构建了本文的数据集。

　　表1 分组密码算法参数表

　　| 密码算法 | 密钥长度/bit | 算法结构 | 加密模式 | 实现方式 |

　　| ---- | ---- | ---- | ---- | ---- |

　　| DES | 56 | Feistel | ECB | Crypto |

　　| AES | 128 | SPN | ECB | Crypto |

　　| 3DES | 168 | Feistel | ECB | Crypto |

　　| Blowfish | 128 | Feistel | ECB | Crypto |

　　| RC2 | 128 | Feistel | ECB | Crypto |

　　| IDEA | 128 | SPN | ECB | OpenSSL |

　　| CAST | 128 | Feistel | ECB | OpenSSL |

　　| SM4 | 128 | Feistel | ECB | OpenSSL |

　　本方案通过编写GM/T0005-2021标准的Python代码实现特征提取器来对密文进行特征提取，该特征提取器包含十五个检测项，通过检测项计算得到p_value值。为了增加特征向量的维度，本文对原有十五种检测项中的部分检测项进行了参数设置[9]，如其中游程分布检测设置针对长度为2到10的游程进行检测，则该检测返回9个值;扑克检测中设置(m=2,4,8)，则该检测返回3个值;设定二元推导检测中参数(k=7)，每进行一次推导返回一个对应的值，即进行7次推导后，返回7个值;设置自相关检测的参数d分别等于1,2,4,8,10,16，即可返回6个p值;近似熵检测的参数为(m=2)和(m=5)，则此检测可以返回两个值。由此共可获得42维特征向量，具体参数设置和检测项简介如表2所示。

　　表2 随机性检测方法参数表

　　| 检测项 | 检测参数 | 返回值数 |

　　| ---- | ---- | ---- |

　　| 单比特频数检测 | - | 1 |

　　| 块内频数检测 | (m=1000,2000,3000,5000) | 4 |

　　| 扑克检测 | (m=2,4,8) | 3 |

　　| 重叠子序列检测 | (m=3,5) | 1 |

　　| 游程总数检测 | - | 1 |

　　| 游程分布检测 | 长度2-10 | 9 |

　　| 块内最大游程检测 | (m=500,5000) | 2 |

　　| 二元推导检测 | (k=7) | 7 |

　　| 自相关检测 | (d=1,2,4,8,10,16) | 6 |

　　| 矩阵秩检测 | - | 1 |

　　| 累加和检测 | - | 2 |

　　| 近似熵检测 | (m=2,5) | 2 |

　　| 线性复杂度检测 | (m=500,1000) | 1 |

　　| Maurer 通用统计检测 | (L=7,Q=1280) | 1 |

　　| 离散傅立叶检测 | - | 1 |

　　4.2 评估标准

　　在分类问题评价标准中，最常用的标准为准确率、精确率、召回率、F1分数[26]。

　　(1)准确率(Accuracy)：准确率是模型预测正确的样本数占总样本数的比例。

　　[Accuracy =frac{TP+TN}{TP+TN+FP+FN}]

　　(2)精确率(Precision)：是指所有被预测为正类的样本中实际为正类的比例。

　　[Precision =frac{TP}{TP+FP}]

　　(3)召回率(Recall)：是指所有实际为正类的样本中被正确预测为正类的比例。

　　[Recall =frac{TP}{TP+FN}]

　　(4)F1分数：是精确率和召回率的调和平均数，是权衡精确率和召回率的一个综合指标。

　　[F_{1}=frac{2TP}{2TP+FP+FN}]

　　在本研究中以准确率和F1分数为主要评估标准。

　　4.3 特征分布

　　本文分别对DES、AES、3DES、Blowfish、IDEA、CAST、SM4、RC2的密文文件进行随机性测试分析，得到这些分组算法密文文件的P_value值。本研究选取块内频数检测在分块为2000bit下绘制特征分布图，横坐标为P_value值，纵坐标为文本数量，如图4所示。在块内频数检测的条件下差异化明显，Blowfish和IDEA算法的文本数量随着P_value值的增加而减少，DES、SM4、RC2、CAST算法的文本数量随着P_value值的增加而增加，尤其是DES算法在P_value值为0.9~1.0范围内增加显著。

　　(图4 特征分布图)

　　4.4 分类识别结果与分析

　　在本研究分类识别部分中，首先进行了DES、AES、3DES、Blowfish、IDEA、CAST、SM4、RC2八种分组密码算法的两两识别，每个密码算法的密文为2000个，且均在ECB模式下加密生成，每个密文大小为32KB。为充分利用数据并且减少过拟合，本方案使用十折交叉验证进行分类实验。

　　如表3所示，本方案两两识别准确率和F1分数均取得了不错的效果，仅有4组两两识别结果为80%以上，其余均在90%以上。其中十一组两两识别对比实验准确率在98%以上，此外，F1分数也与准确率呈现相同的规律，说明模型稳定性良好。实验结果如表4所示，所得实验结果整体均高于四个对比文献，相较参考文献本方案得到的实验结果整体准确率提升约12%。

　　表3 RF-LightGBM方案两两识别结果

　　| 算法 | 准确率/% | F1 分数/% | 算法 | 准确率/% | F1 分数/% |

　　| ---- | ---- | ---- | ---- | ---- | ---- |

　　| 3DES vs AES | 98.75 | 98.60 | Blowfish vs DES | 93.37 | 92.17 |

　　| 3DES vs Blowfish | 94.63 | 94.68 | Blowfish vs IDEA | 91.87 | 91.40 |

　　| 3DES vs CAST | 89.85 | 88.79 | Blowfish vs RC2 | 90.90 | 89.02 |

　　| 3DES vs DES | 90.13 | 89.80 | Blowfish vs SM4 | 98.25 | 98.13 |

　　| 3DES vs IDEA | 90.00 | 89.55 | CAST vs DES | 93.25 | 93.52 |

　　| 3DES vs RC2 | 87.50 | 86.62 | CAST vs IDEA | 92.25 | 91.80 |

　　| 3DES vs SM4 | 97.87 | 97.73 | CAST vs RC2 | 92.25 | 91.92 |

　　| AES vs Blowfish | 98.12 | 98.04 | CAST vs SM4 | 99.25 | 99.80 |

　　| AES vs CAST | 98.50 | 97.63 | DES vs IDEA | 93.64 | 92.08 |

　　| AES vs DES | 98.87 | 98.81 | DES vs RC2 | 89.87 | 89.26 |

　　| AES vs IDEA | 99.12 | 99.07 | DES vs SM4 | 98.37 | 98.13 |

　　| AES vs RC2 | 99.12 | 98.94 | IDEA vs RC2 | 90.25 | 90.87 |

　　| AES vs SM4 | 85.63 | 86.31 | IDEA vs SM4 | 98.37 | 98.56 |

　　| Blowfish vs CAST | 92.50 | 91.97 | RC2 vs SM4 | 98.62 | 98.55 |

　　表4 方案结果对比

　　| 识别方案 | 样本长度 | 准确率范围/% |

　　| ---- | ---- | ---- |

　　| 文献[9] | 512kb | 45-89 |

　　| 文献[12] | 512KB | 80-89 |

　　| 文献[16] | 1-512KB | 80-84 |

　　| 文献[13] | 1MB | 82-88 |

　　| 本文 | 32KB | 85-99 |

　　为了进一步验证本文方案的识别效果，本研究继续对多个分组密码算法的多分类识别测试。在相同条件下分别采用RF-LightGBM模型和随机森林模型进行实验。在评估过程中，采用宏平均指标来计算F1值和准确率，以确保每个类别的性能都能得到公平且准确的评估。图5给出了RF-LightGBM模型八分类情况下测试结果的混淆矩阵。

　　表5给出了RF-LightGBM模型和随机森林模型多分类识别结果的对比。其中，RF-LightGBM模型的三分类识别准确率为91.01%，四分类准确率为89.67%，五分类准确率为84.37%，六分类准确率为81.85%，七分类准确率为77.08%，八分类准确率为73.60%。实验结果表明，随机森林模型方案的多分类实验结果准确率和F1分数均低于RF-LightGBM模型方案。

　　(图5 八分类混淆矩阵图)

　　表5 多分类识别方案对比

　　| 分类 | RF-LightGBM准确率/% | RF-LightGBM F1度量/% | 随机森林准确率/% | 随机森林F1度量/% |

　　| ---- | ---- | ---- | ---- | ---- |

　　| 三分类 | 91.01 | 90.74 | 85.73 | 84.12 |

　　| 四分类 | 89.67 | 89.63 | 82.87 | 81.64 |

　　| 五分类 | 84.37 | 84.36 | 76.37 | 77.12 |

　　| 六分类 | 81.85 | 81.84 | 73.23 | 72.48 |

　　| 七分类 | 77.08 | 76.97 | 70.31 | 69.45 |

　　| 八分类 | 73.60 | 72.65 | 64.37 | 63.77 |

　　5 总结

　　为解决分组密码识别的短样本识别需求以及进一步提高识别准确率，本文提出一种基于RF-LightGBM的分组密码体制识别方案，解决短样本识别需求以及利用未知密文识别分组密码加密结构的问题。使用DES、AES、3DES、Blowfish、IDEA、CAST、SM4、RC2八种分组密码算法对每个大小为32KB的明文在ECB模式下进行加密得到密文。通过GM/T0005-2021特征提取器对其密文进行特征提取，将特征向量输入随机森林算法模型进行排序和筛选，将筛选后的特征向量输入进LightGBM分类器进行两两识别测试。在八种分组密码相互两两识别结果中，有四组密码算法的识别准确率在80%~90%，其余二十四组密码算法的识别率均在90%以上。相较于现有方案结果，本方案整体识别准确率约提高12%。其次，本文又对八种分组密码进行了多分类实验，并且在相同条件下对随机森林模型进行测试，本方案所得实验结果均高于对比模型。其中，本方案八分类的识别准确率为73.60%。以上实验结果验证了GM/T0005-2021标准作为提取较短样本长度特征向量的可行性，以及RF-LightGBM方案识别效果的优越性。

　　在后续的研究工作中，可以进一步研究更小的样本长度以及加密分组长度对识别准确率的影响，并且尝试对CBC、CFB等复杂工作模式开展研究，继续优化密文特征选择和特征处理过程。

　　参考文献

　　[1] Maqsood F, Ahmed M, Ali M M, et al. Cryptography: a comparative analysis for modern techniques[J]. International Journal of Advanced Computer Science and Applications, 2017, 8(6).

　　[2] 李瑞林. 分组密码的分析与设计[D]. 国防科学技术大学, 2011.

　　[3] 赵志诚. 基于机器学习的密码体制识别研究[D]. 郑州: 信息工程大学, 2018.

　　[4] 张永强, 李顺波, 屈帅, et al. NIST随机性检测方法及应用[J]. 电脑知识与技术, 2014, (9X):6064-6066.

　　[5] GM/T0005-2021, 随机性检测规范[S].

　　[6] 付文博, 孙涛, 梁藉, et al. 深度学习原理及应用综述[J]. 计算机科学, 2018, 45(B06):11-15.

　　[7] 黄良韬, 赵志诚, 赵亚群. 基于随机森林的密码体制分层识别方案[J]. 计算机学报, 2018, 41(2):382-399.

　　[8] 赵志诚, 赵亚群, 刘凤梅. Grain-128算法的密码体制识别研究[J]. 信息工程大学学报, 2019, 20(1):102-110.

　　[9] 赵志诚, 赵亚群, 刘凤梅. 基于随机性测试的分组密码体制识别方案[J]. 密码学报, 2019, 6(2):177-190.

　　[10] 纪文桃, 李媛媛, 秦宝东. 基于随机性特征的SM4分组密码体制识别[J]. Application Research of Computers/Jisuanji Yingyong Yanjiu, 2021, 38(9).

　　[11] 曹莉茹. 基于深度学习的密码算法识别研究[D]. 电子科技大学, 2021.

　　[12] 刘节威, 王钢, 颜培志, et al. 基于CNN的国产商用分组密码算法识别研究[J]. 网络安全与数据治理, 2022, 41(9):7-14.

　　[13] Ruiqi X, Manman L, Shaozhen C. Encryption Modes Identification of Block Ciphers based on Machine Learning[J]. International Journal of Network Security & Its Applications, 2022, 14(5):1-10.

　　[14] Yuan K, Huang Y, Li J, et al. A block cipher algorithm identification scheme based on hybrid random forest and logistic regression model[J]. Neural Processing Letters, 2023, 55(3):3185-3203.

　　[15] 夏锐琪, 李曼曼, 陈少真. 基于机器学习的分组密码结构识别[J]. 网络与信息安全学报, 2023, 9(03):79-89.

　　[16] 张运理, 石元兵, 明爽, et al. 唯密文场景下的分组密码算法识别方法[J]. 通信技术, 2024, (002):057-064.

　　[17] 陈慧锋. 基于深度学习的轻量级分组密码研究[D]. 中国矿业大学, 2023. DOI:10.27623/d.cnki.gzkyu.2023.003102.

　　[18] 李洪超. 基于密文特征的密码算法识别研究[D]. 西安: 西安电子科技大学, 2018.

　　[19] LI Z-s, YAO X, LIU Z-g, et al. Feature selection algorithm based on LightGBM[J]. Journal of Northeastern University (Natural Science), 2021, 42(12):1688-1694.

　　[20] Parmar A, Katariya R, Patel V. A review on random forest: An ensemble classifier[C]. Proceedings of the International conference on intelligent data communication technologies and internet of things (ICICI) 2018, F, 2019. Springer.

　　[21] Vens C, Costa F. Random forest based feature induction[C]. Proceedings of the 2011 IEEE 11th international conference on data mining, F, 2011. IEEE.

　　[22] Ke G, Meng Q, Finley T, et al. Lightgbm: A highly efficient gradient boosting decision tree[J]. Advances in neural information processing systems, 2017, 30.

　　[23] Wang D-n, Li L, Zhao D. Corporate finance risk prediction based on LightGBM[J]. Information Sciences, 2022, 602:259-268.

　　[24] Al Daoud E. Comparison between XGBoost, LightGBM and CatBoost using a home credit dataset[J]. International Journal of Computer and Information Engineering, 2019, 13(1):6-10.

　　[25] Hancock J, Khoshgoftaar T M. Leveraging lightgbm for categorical big data[C]. Proceedings of the 2021 IEEE Seventh International Conference on Big Data Computing Service and Applications (BigDataService), F, 2021. IEEE.

　　[26] Yuan K, Yu D, Feng J, et al. A block cipher algorithm identification scheme based on hybrid k-nearest neighbor and random forest algorithm[J]. PeerJ Computer Science, 2022, 8:e1110.

　　英文摘要

　　Identification Scheme for Block Cipher Algorithms Based on RF-LightGBM

　　DONG Xiuze YANG Honggang HU Yifan YU Gengchen

　　Beijing Electronic Science and Technology Institute, Beijing 100070, P.R. China

　　Abstract: Cryptographic algorithm identification holds significant importance in the cryptanalysis field. In mainstream block cipher algorithm identifying schemes, the ciphertext feature extraction is typically based on randomness detection standards. To address the need for identifying short samples and further improve the identification accuracy, an identification scheme for block cipher systems based on RF-LightGBM is proposed in this paper. Firstly, ciphertext features are extracted according to the GM/T 0005-2021 randomness detection standard, and the Random Forest algorithm is utilized to rank and filter the importance of high-dimensional data. Then, feature vectors are used to train a LightGBM model to construct a cryptographic algorithm classifier for identification. This method fulfills the need for efficiently identifying unknown ciphertexts under short sample conditions. The proposed scheme achieves an overall accuracy enhancement of about 12% in pairwise identification experiments, outperforming existing schemes. Multi-classification experiments show that the accuracy rates exceed 73%, verifying the effectiveness and superiority of the proposed scheme in block cipher algorithms identification, which provides a valuable reference for future cryptographic algorithm identifying under more complex encryption modes.

　　Keywords: block cipher; machine learning; randomness detection; cryptographic algorithm identification; LightGBM