摘要:摘要:为解决传统压水堆辐照监督理论计算中多次物理建模、粒子输运计算及效率低的问题,基于蒙特卡罗(MC)方法与离散纵标(SN)方法耦合的正向权重一致共轭驱动重要性抽样(FW-CADIS)方法,建
摘要:为解决传统压水堆辐照监督理论计算中多次物理建模、粒子输运计算及效率低的问题,基于蒙特卡罗(MC)方法与离散纵标(SN)方法耦合的正向权重一致共轭驱动重要性抽样(FW-CADIS)方法,建立压力容器辐照监督管中子注量计算的加速方法。在某CPR1000机组中开展计算精度和速度的影响因素研究,验证该方法在不同堆芯参数下的适用性并给出SN输运模拟参数建议值;通过该机组验证与确认,结果表明:与直接MC方法相比,中子注量率计算的品质因子(FOM)提高约95~181倍;中子注量计算结果与实测值的相对偏差不超过8%。该方法可显著提高计算效率,同时满足工程应用的精度要求。
关键词:中子注量;辐照监督;压水堆;正向权重一致共轭驱动重要性抽样(FW-CADIS);蒙特卡罗(MC)
论文《压水堆辐照监督理论计算的加速方法及验证》发表在《核动力工程》,版权归《核动力工程》所有。本文来自网络平台,仅供参考。
1 引言
压水堆运行过程中,反应堆压力容器(RPV)长期受中子辐照会产生辐照损伤,影响结构完整性和使用寿命[1-2]。辐照监督作为评估压力容器辐照损伤的关键手段,通过在压力容器内壁布置辐照监督管,监测中子注量并推断压力容器的实际辐照水平,为设备寿命评估提供依据[3-4]。
传统辐照监督理论计算主要依赖蒙特卡罗(MC)粒子输运方法,需对每根监督管在每个燃料循环的辐照情况单独建模计算,存在多次物理建模、粒子输运计算量大、计算效率低等问题[5-6]。离散纵标(SN)方法计算速度快、易收敛,但精度相对较低[7-8]。正向权重一致共轭驱动重要性抽样(FW-CADIS)方法通过耦合MC与SN方法,利用SN方法快速获取减方差参数,可显著降低MC计算的统计方差,提高收敛速度[9-10]。
本文基于FW-CADIS方法,结合堆芯核设计程序PCM、SN程序JSNT和MC程序JMCT,建立压水堆辐照监督理论计算的加速方法,通过CPR1000机组验证其准确性和高效性,为工程应用提供技术支撑。
2 理论基础与实现过程
2.1 FW-CADIS方法原理
FW-CADIS方法核心是通过SN方法计算正向和共轭中子注量率分布,生成MC计算所需的减方差参数(源偏倚因子、权窗因子),从而加速MC计算收敛,具体步骤如下:
1. SN正向输运计算:建立SN物理模型,开展正向中子输运计算,获取粗略的正向中子注量率分布(phi(r, E, Omega)),并根据式(4)确定共轭源分布(q^+(r, E, Omega)):
[q^{+}(r, E, Omega)=frac{sigma(r, E, Omega)}{iint phi(r, E, Omega) sigma(r, E, Omega) d E d Omega} ag{4}]
式中,(sigma(r, E, Omega))为截面分布。
2. SN共轭输运计算:基于共轭源分布(q^+(r, E, Omega))开展SN共轭输运计算,获得共轭中子注量率分布(phi^+(r, E, Omega)),并通过式(5)、(6)计算源偏倚因子(hat{q}(r, E, Omega))和权窗因子(w(r, E, Omega)):
[hat{q}(r, E, Omega)=frac{phi^{+}(r, E, Omega) q(r, E, Omega)}{iiint phi^{+}(r, E, Omega) q(r, E, Omega) d r d E d Omega} ag{5}]
[w(r, E, Omega)=frac{iiint phi^{+}(r, E, Omega) q(r, E, Omega) d r d E d Omega}{phi^{+}(r, E, Omega)} ag{6}]
式中,(q(r, E, Omega))为原始源分布。
3. MC正向输运计算:将减方差参数代入MC物理模型,开展正向中子输运计算,实现结果快速收敛。
2.2 辐照监督计算理论基础
压力容器辐照监督计算属于纯外源问题,通过堆芯功率分布构造源分布,采用MC程序固定源模式计算辐照监督管和压力容器的中子注量率分布,结合运行历史得到累积中子注量,具体计算过程如下:
1. 累积中子注量计算:
[Psi_{calc}=int phi_{calc}left(t_{i}
ight) d t_{i} ag{7}]
式中,(Psi_{calc})为累积中子注量理论计算值,(phi_{calc}(t_i))为第(i)个燃料循环的中子注量率计算值,(t_i)为第(i)个燃料循环的辐照时间。
2. 超前因子计算:
[L=frac{Psi_{ISC, calc}}{Psi_{RPV, calc}} ag{8}]
式中,(L)为超前因子,(Psi_{ISC, calc})、(Psi_{RPV, calc})分别为辐照监督管和压力容器的累积中子注量理论计算值。
3. 压力容器实际中子注量推断:
[Psi_{RPV, mes}=frac{Psi_{ISC, mes}}{L} ag{9}]
式中,(Psi_{ISC, mes})为辐照监督管累积中子注量实测值,(Psi_{RPV, mes})为压力容器累积中子注量实际值。
工程中需计算能量大于0.1 MeV和1 MeV的中子注量,用于辐照损伤评估。
2.3 加速计算方法实现过程
基于FW-CADIS的辐照监督加速计算流程分为4个步骤,如图1所示:
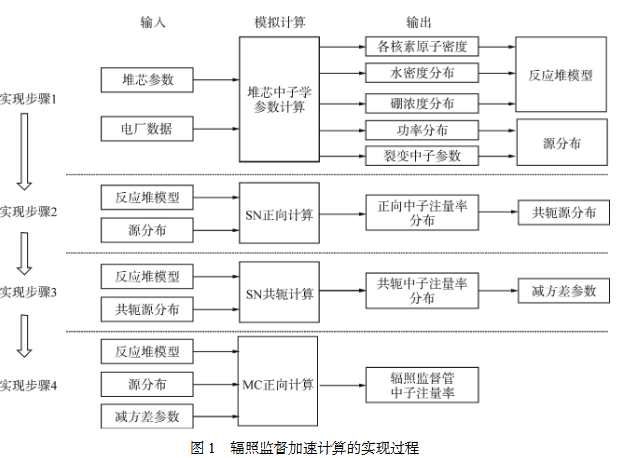
[图1 加速计算方法实现流程]
1. 堆芯中子学参数计算及物理建模:基于堆芯参数和实测通量图数据,使用PCM程序进行燃耗-输运耦合计算,得到各循环不同燃耗下的原子密度、水密度、硼浓度、功率分布及裂变中子参数,用于构建粒子输运模拟的物理模型和源分布(空间分布、能谱)。
2. SN正向计算:建立通用SN几何模型(无需精细建模,采用典型几何参数),堆芯物理参数采用循环燃耗加权平均值替代,具体加权公式如下:
[M=frac{sum_{i}left(t_{i} × frac{sum_{j} B_{i j} m_{i, j}}{sum_{j} B_{i j}}
ight)}{sum_{i} t_{i}} ag{10}]
式中,(M)为加权平均参数,(t_i)为第(i)个循环的辐照时间,(B_{ij})为第(i)个循环第(j)个燃耗步的燃耗深度,(m_{i,j})为第(i)个循环第(j)个燃耗步的参数值。
3. SN共轭计算:基于SN正向计算结果,构造共轭源分布,开展SN共轭输运计算,生成MC计算所需的减方差参数。
4. MC正向计算:将减方差参数代入MC模型,开展正向中子输运计算,得到辐照监督管中子注量率分布。
3 辐照监督加速计算与验证
3.1 反应堆模型
基于某CPR1000机组的真实堆芯物理参数、几何参数和材料参数,使用JSNT/JMCT程序建立1/4堆芯粒子输运物理模型(选取含2根辐照监督管的象限),反应堆径向部件从内到外依次为燃料组件、围板、吊篮、热屏、辐照监督管、压力容器、保温层。堆芯燃料组件为AFA3G型(共157个),采用均匀化模型;辐照监督管采用精细化建模,包含包容器、壳体、底架、力学性能试样及上中下三个中子探测器。
[图2 CPR1000的计算模型剖面图]
(a)X-Y平面剖面图;(b)X-Z平面剖面图
3.2 影响因素分析
3.2.1 堆芯物理参数影响分析
选取水密度、燃耗分布、功率分布、能谱、硼浓度等典型堆芯物理参数,开展敏感性分析,比较加速方法与直接MC方法的中子注量率计算结果,如表1所示。结果表明:在典型堆芯参数变化范围内,两种方法的计算偏差均在3倍统计误差(3σ)以内,证明加速方法在不同堆芯状态下具有准确性和无偏性。
表1 堆芯参数敏感性分析
| 参数类型 | 变化类型 | 统计误差/% | | 计算偏差/% |
| | | 加速方法 | 直接MC方法 | |
| 水密度变化 | -0.2 g/cm³ | 0.52 | 1.04 | 0.53 |
| | -0.1 g/cm³ | 0.57 | 1.16 | -0.56 |
| | 0 g/cm³ | 0.62 | 1.30 | -0.87 |
| | 0.1 g/cm³ | 0.69 | 1.43 | 0.01 |
| | 0.2 g/cm³ | 0.74 | 1.56 | 1.05 |
| 燃耗分布 | 第1循环 | 0.63 | 1.35 | 1.18 |
| | 第2循环 | 0.63 | 1.36 | 1.90 |
| | 第3循环 | 0.62 | 1.35 | 2.33 |
| | 第4循环 | 0.62 | 1.35 | 2.54 |
| 功率分布 | 第1循环 | 0.62 | 1.30 | -0.87 |
| | 第2循环 | 0.64 | 1.33 | -1.95 |
| | 第3循环 | 0.63 | 1.29 | 0.32 |
| | 第4循环 | 0.63 | 1.30 | -0.48 |
| 能谱 | 第1循环 | 0.62 | 1.30 | -0.87 |
| | 第2循环 | 0.62 | 1.31 | 0.19 |
| | 第3循环 | 0.62 | 1.29 | -1.23 |
| | 第4循环 | 0.62 | 1.28 | -1.46 |
| | 瓦特谱 | 0.63 | 1.31 | -0.60 |
| 硼浓度变化 | -200 ppm | 0.62 | 1.30 | 1.80 |
| | -100 ppm | 0.62 | 1.30 | 0.10 |
| | 0 ppm | 0.62 | 1.30 | -0.72 |
| | 100 ppm | 0.62 | 1.29 | 0.21 |
| | 200 ppm | 0.62 | 1.30 | 0.83 |
(注:1 ppm=10⁻⁶)
3.2.2 SN模拟参数影响分析
SN模拟的离散角度和空间离散尺寸直接影响减方差参数质量,进而影响MC计算效果:
1. 离散角度影响:选取S2、S4、S8、S16四种离散角度,空间离散尺寸均为2 cm,分析对MC收敛速度和计算结果的影响(表2)。结果表明:不同离散角度下,中子注量率偏差均在3σ以内;离散角度对SN计算时间影响显著,S2离散角度的SN计算时间仅148 s,建议优先选择S2~S4离散角度以节约计算时间。
表2 不同角度离散数对计算结果的影响
| 角度离散数 | SN计算时间/s | 模拟粒子数为10⁵ | | 模拟粒子数为10⁷ | |
| | | 统计误差/% | 中子注量率偏差/% | 统计误差/% | 中子注量率偏差/% |
| S2 | 148 | 4.76 | 0.08 | 0.68 | 0.49 |
| S4 | 279 | 4.49 | 0.51 | 0.64 | -0.11 |
| S8 | 718 | 4.14 | -5.56 | 0.62 | 0.06 |
| S16 | 2378 | 4.23 | -3.89 | 0.63 | -0.84 |
2. 空间离散尺寸影响:选取2、3、5、10、15、20 cm六种空间离散尺寸,角度离散数为S16,分析对MC收敛速度和计算结果的影响(表3)。结果表明:空间离散尺寸越小,MC收敛速度越快,但SN计算时间越长;空间离散尺寸过大(如20 cm)会导致减方差效果下降;建议选择5~10 cm的空间离散尺寸,兼顾SN计算效率和MC收敛速度。
表3 不同空间离散尺寸对计算结果的影响
| 空间离散尺寸/cm | 总网格数 | SN计算时间/s | 统计误差/% | 中子注量率偏差/% |
| 2 | 4.0×10⁶ | 19789 | 0.60 | 0.38 |
| 3 | 1.2×10⁶ | 7894 | 0.62 | -0.34 |
| 5 | 2.2×10⁵ | 2378 | 0.63 | -0.84 |
| 10 | 2.8×10⁴ | 2407 | 0.81 | 0.04 |
| 15 | 1.2×10⁴ | 2388 | 1.17 | -2.21 |
| 20 | 3.5×10³ | 2841 | 3.87 | -3.09 |
3.3 验证与确认
在CPR1000机组中开展加速方法的验证与确认,对比加速方法与直接MC方法的计算效率和精度:
1. 计算效率对比:直接MC方法模拟粒子数为10⁹,CPU核数80个;加速方法中MC模拟粒子数为10⁷,SN计算角度离散数S4、空间离散尺寸5 cm。结果表明(表4):加速方法的FOM提高95~181倍,统计误差均低于1%,满足工程要求(统计误差<5%);直接MC方法需约1 h收敛至统计误差5%,而加速方法仅需30 s以内(图5)。
表4 两种方法快中子注量理论计算值的对比
| 燃料循环 | 模拟方法 | 统计误差/% | 计算时间/h | FOM | 计算偏差/% | FOM比值 |
| 第1循环 | 直接MC方法 | 0.47 | 94.16 | 6.06 | 0.63 | 150 |
| | 加速方法 | 0.60 | 0.38 | 907.68 | - | - |
| 第2循环 | 直接MC方法 | 0.34 | 133.86 | 8.27 | 1.28 | 113 |
| | 加速方法 | 0.60 | 0.37 | 935.59 | - | - |
| 第3循环 | 直接MC方法 | 0.33 | 229.45 | 5.16 | 0.30 | 181 |
| | 加速方法 | 0.60 | 0.37 | 932.42 | - | - |
| 第4循环 | 直接MC方法 | 0.46 | 67.20 | 8.72 | 0.90 | 95 |
| | 加速方法 | 0.60 | 0.43 | 826.38 | - | - |
[图5 直接MC方法与加速方法的收敛速度对比]
2. 计算精度对比:将累积中子注量理论计算值与实测值对比(表5),加速方法的计算偏差不超过8%,符合工程级精度要求。
表5 累积中子注量理论计算值与实测值的对比
| 探测器位置 | 能量范围 | 计算值与实测值偏差/% | |
| | | 直接MC方法 | 加速方法 |
| 上 | E>1.0 MeV | 6 | 5 |
| | E>0.1 MeV | 2 | 1 |
| 中 | E>1.0 MeV | 6 | 8 |
| | E>0.1 MeV | 3 | 4 |
| 下 | E>1.0 MeV | 8 | 6 |
| | E>0.1 MeV | 7 | 7 |
4 结论
本文基于FW-CADIS方法,耦合MC与SN方法,建立了压水堆辐照监督理论计算的加速方法,通过CPR1000机组验证得到以下结论:
1. 加速方法的减方差参数在不同堆芯物理参数(水密度、燃耗分布、功率分布等)下具有广泛适用性,无需重复SN建模和减方差参数计算,可直接用于不同堆芯状态的MC加速计算。
2. 给出SN模拟参数建议值:角度离散数选取S2~S4,空间离散尺寸选取5~10 cm,兼顾计算效率和精度。
3. 与直接MC方法相比,加速方法的FOM提高95~181倍,计算时间显著缩短;中子注量计算结果与实测值偏差不超过8%,满足工程应用精度要求。
该方法可有效解决传统辐照监督计算效率低的问题,尤其适用于多循环、多迭代设计场景,为压水堆辐照监督理论计算提供高效可行的技术方案。
参考文献
[1] 能源行业核电标准化技术委员会. 轻水冷却反应堆压力容器辐照监督:NB/T 20220-2013[S]. 北京:核工业标准化研究所,2013:1-25.
[2] 张斌,郑君萧,李晓静,等. 反应堆压力容器快中子注量计算不确定性分析[J]. 核技术,2018,41(2):020605.
[3] 许怀金. RPV快中子注量率计算评估方法研究[D]. 北京:华北电力大学(北京),2022.
[4] 郑君萧. 基于SN方法的反应堆压力容器快中子注量率计算方法研究[D]. 北京:华北电力大学(北京),2017.
[5] 夏春梅,梅其良,丁谦学,等. DORT程序进行RPV中子注量率计算的可靠性验证[J]. 核科学与工程,2016,36(3):329-334.
[6] VASILIEV A, FERROUKHI H, ZIMMERMANN M A, et al. Development of a CASMO-4/SIMULATE3/MCNPX calculation scheme for PWR fast neutron fluence analysis and validation against RPV scraping test data[J]. Annals of Nuclear Energy, 2007, 34(8):615-627.
[7] 靳忠敏,陈义学,石生春,等. 基于MCNP的压力容器快中子注量率计算参数敏感性分析[J]. 原子能科学技术,2011,45(2):195-199.
[8] 石秀安,苏耿华,包鹏飞. 压水堆辐照监督管中子注量计算方法改进研究[J]. 核科学与工程,2018,38(4):585-589.
[9] 邓理邻,吕焕文,谭怡,等. 辐照监督管中子注量率精细化模型计算方法研究[J]. 核动力工程,2013,34(S1):84-86.
[10] 刘巧凤,韩静茹. CAP1400反应堆压力容器快中子注量独立审核计算[J]. 中国核电,2018,11(4):462-465.
[11] TIEP N H, HOANG S M T, HARTANTO D, et al. Investigation of the VVER-1000 reactor pressure vessel neutron fluence and displacement per atom using MCNP6[J]. Radiation Physics and Chemistry, 2020, 177:109141.
[12] NGUYEN H T, NHU V H P, NGUYEN M T. Calculation of neutron and gamma fluences on VVER reactor pressure vessel[J]. Nuclear Science and Technology, 2016, 6(4):18-25.
[13] ARDEKANI S F G, HADAD K. Monte Carlo evaluation of neutron irradiation damage to the VVER1000 RPV[J]. Nuclear Energy and Technology, 2017, 3(2):73-80.
[14] 李刚,张宝印,邓力,等. 蒙特卡罗粒子输运程序JMCT研制[J]. 强激光与粒子束,2013,25(1):158-162.
[15] 邓力,李刚,张宝印,等. JMCT蒙特卡罗中子-光子输运程序全堆芯pin-by-pin模型的模拟[J]. 原子能科学技术,2014,48(6):1061-1066.
[16] 邓力,李瑞,丁谦学,等. 基于JMCT秦山核电厂一期反应堆屏蔽计算与分析[J]. 核动力工程,2021,42(2):173-179.
[17] 李刚,邓力,张宝印,等. BEAVRS基准模型热零功率状态的JMCT分析[J]. 物理学报,2016,65(5):052801.
[18] 刘雄国,邓力,胡泽华,等. 基于VENUS-Ⅲ国际基准模型的JMCT程序验证[J]. 计算物理,2016,33(5):570-580.
[19] 杨超,程汤培,邓力,等. 三维并行程序JSNT对HBR-2装置的屏蔽计算与分析[J]. 原子能科学技术,2019,53(2):250-255.
[20] 张广春,程汤培,邓力,等. 基于JSNT程序的压水堆屏蔽计算[J]. 强激光与粒子束,2017,29(3):036020.
[21] 史涛. 蒙特卡罗粒子输运问题中的减方差方法研究[D]. 绵阳:中国工程物理研究院,2018.
[22] 王超,邓力. 基于MCNP多群伴随计算与正算分析的比较[J]. 原子核物理评论,2012,29(4):388-394.
[23] WAGNER C J, PEPLOW E D, MOSHER W S. FW-CADIS method for global and regional variance reduction of Monte Carlo radiation transport calculations[J]. Nuclear Science and Engineering, 2014, 176(1):37-57.





