计及限流切换的构网型变换器并联系统暂态同步稳定分析

　　电网短路故障下，并联运行的新能源构网型变换器暂态交互作用显著增强，增加了系统暂态同步失稳风险。文中首先建立了构网型变换器并联系统暂态交互模型。其次，借助传统同步发电机稳定理论，分析了暂态交互能量影响变换器稳定性的作用机理，进一步揭示了交互能量作用下的功角牵引机制将促使多变换器稳定性趋近一致或致使稳定性较差的变换器加速失稳。由此，提出了计及限流切换的构网型变换器并联系统稳定域构建方法，并通过稳定域分析了变换器运行状态及控制参数对系统暂态稳定性的影响规律。最后，仿真和实验结果验证了理论分析的正确性。

　　关键词：构网型变换器;暂态稳定;并联运行;暂态交互能量;稳定域;限流

　　论文《计及限流切换的构网型变换器并联系统暂态同步稳定分析》发表在《电力系统自动化》，版权归《电力系统自动化》所有。本文来自网络平台，仅供参考。

　　0 引言

　　大力发展风、光等新能源是中国实现“双碳”战略目标的重要举措，截至2023年底，风电、光伏发电的装机容量为1.05 TW，占比达到36%，发电量为1200 TW·h，占比达到15.3%[1]。预计到2030年，风电、光伏发电装机容量占比和发电量占比将分别达到40%和20%[2]。基于跟网型(grid-following, GFL)控制架构的大规模新能源经电力电子变换器(下文简称“变换器”)接入电网导致同步发电机主导的电网稳定特性发生显著变化[3]，暂态、动态主动支撑能力持续减弱[4]，给电网安全稳定运行带来严峻挑战。借鉴同步发电机物理机理、能够自主建立交流电压并通过自身输出功率实现与交流电网同步的构网型(grid-forming, GFM)变换器被视为解决上述问题的有效手段之一[5]。

　　虽然借鉴了同步发电机物理机理，但是构网型变换器暂态稳定动力学特性相比同步发电机更为复杂：一方面，构网型变换器控制架构多样[5-7]，且控制参数选取不受物理限制、灵活性较高[8];另一方面，构网型变换器故障下切换为限流控制模式，功角特性曲线复杂多变[9-10]。因此，构网型变换器暂态同步稳定分析结论并不能直接套用同步发电机。近年来，国内外学者围绕构网型变换器同步控制架构、内外环方案、限流策略对暂态同步稳定性的影响以及暂态稳定性提升策略展开了大量研究，并取得了诸多研究成果。文献[11]研究了故障后平衡点是否存在对稳定性的影响，提出了提升暂态稳定性的控制器设计方法;文献[12-13]通过临界切除角和临界切除时间量化分析了不同同步控制环节、无功电压控制环节、内外环对暂态稳定性的影响，并通过功角特性揭示了构网型变换器暂态失稳机理。文献[14]研究了限流模式对变换器暂态稳定性的影响，并给出了提升临界切除时间的限流模式下最优电流相位角。上述研究均以单构网型变换器并网系统为研究对象，其结论无法直接拓展到多变换器系统中。

　　未来，构网型变换器并联运行场景将广泛存在于新能源场站内。从广义上讲，新能源基地多个构网型场站的并列运行也属于该范畴。已有研究表明，变换器并联运行暂态交互作用显著，交互耦合路径不仅存在于变换器与电网间，还存在于变换器间[15-16]。更为重要的是，变换器暂态交互还受限流模式切换[17]、变换器响应时序不一致[18-19]等问题耦合影响，增加了并联系统分析的困难。现有构网型变换器并联运行研究主要集中在小扰动稳定性，鲜有从系统层面研究大扰动暂态稳定。如文献[18]建立多虚拟同步发电机(virtual synchronous generator, VSG)并联系统的单机等值模型，根据参数灵敏度分析，揭示了系统参数及控制参数对振荡频率的影响规律。文献[20]利用单输入单输出等值模型，并结合奈奎斯特准则，对VSG并网系统进行了稳定性分析。此外，文献[21]提出了微网中VSG协同控制方法，改善了微网中多VSG间暂态失步问题，但缺乏对系统稳定性影响的分析和探讨。文献[22]建立了构网型变换器与跟网型变换器交互模型，发现注入电流对VSG暂态稳定性的影响主要由功率耦合项决定，但未涉及对构网型变换器并联运行暂态稳定性的分析。构建稳定域是分析系统暂态稳定性的有效途径，已有文献通过构建变换器稳定域判断系统的大扰动暂态稳定性[23]，但相关研究聚焦在单台VSG[24]或VSG并联跟网型变换器系统[25]，缺乏计及限流切换的构网型变换器并联运行稳定域构建方法研究。

　　针对上述问题，本文首先建立了构网型变换器并联系统暂态交互模型。其次，借助传统同步发电机稳定理论，分析了暂态交互能量影响变换器稳定性的作用机理，进一步揭示了交互能量作用下的功角牵引机制将促使多变换器稳定性趋近一致或致使稳定性较差的变换器加速失稳。由此，提出了计及限流切换的并联系统稳定域构建方法，并通过稳定域分析了运行状态及控制参数对暂态稳定性的影响规律。最后，仿真和实验结果验证了上述理论分析的正确性。

　　1 变换器并联系统暂态交互模型

　　1.1 同步架构及限流控制模式

　　构网型变换器的同步方式可以依据被控对象分为有功功率同步[26]和直流电压同步[27]两大类。有功功率同步又可细分为下垂控制、虚拟同步控制等。下垂控制仅模拟同步发电机有功-频率一阶下垂特性，虽不存在暂态失稳问题，但缺少有功功率的惯性响应，这对于低惯量电力系统中频率稳定至关重要，有必要保留惯性响应。基于直流电压同步的控制方式会在暂态稳定性分析中引入直流动态，增加研究问题的复杂性。因此，本文采用目前主流的模拟同步发电机转子二阶方程的构网型变换器同步控制架构，其功角特性曲线以及暂态稳定性与同步发电机并无本质不同。但是同步控制参数会影响变换器同步动态，进而对暂态稳定性产生较大影响。同步控制架构如附录A图A1所示。

　　短路故障下构网型变换器同步环节可以使用功率同步环生成参考相位，也可以切换为锁相环提供参考相位[28]，与电网保持同步。切换为锁相环同步时，其稳定动力学模型与跟网型变换器完全等价，虽可以在一定程度上限制故障电流，但锁相环动态的引入将增加故障及恢复过程中暂态同步失稳风险[29]。因此，故障下仍然采用功率同步环生成基准相位，后文均基于此方式进行分析。

　　构网型变换器无功电压控制环节影响电压跌落程度和恢复速度，进而影响暂态稳定性，控制架构如附录A图A2所示。值得注意的是，考虑到短路故障触发电流限幅环节动作情况下，内电势幅值不受无功电压环控制，相当于无功电压环在限流时被旁路，不影响暂态同步稳定分析。

　　短路故障下，变换器功角特性曲线由电流限幅算法决定，合适的电流限幅算法有助于提升暂态同步稳定性。目前，主流的限流算法包括虚拟阻抗限幅[30]和电流内环限幅[14]两类，已有文献证明，虚拟阻抗限幅方法在故障开始的数毫秒内效果不及电流内环限幅控制[17]。因此，本文在电压幅值单环控制的基础上增加电流内环进行故障限流控制，其结构如附录A图A3所示。

　　1.2 并联系统拓扑结构

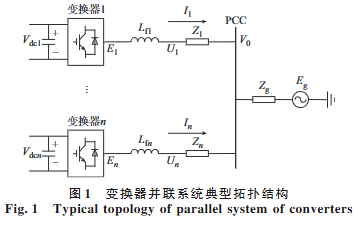
　　构网型变换器并联系统接入电网拓扑结构如图1所示。图中：变换器通过滤波电感(L_{fi})和阻抗为(Z_i)的线路连接到一个公共耦合点(point of common coupling, PCC)母线上，经过线路阻抗(Z_R)与无穷大电网(E_g)连接;(V_{dci})、(E_i)、(U_i)、(I_i)分别为第(i)台变换器的直流侧电压、内电势幅值、端电压幅值、输出电流幅值，其中，(i=1,2,cdots,n)，(n)为变换器数量;(L_{fi})、(Z_i)分别为第(i)台变换器的滤波电感值和所在线路对应的线路阻抗值;(V_0)为PCC的电压幅值。

　　图1 变换器并联系统典型拓扑结构

　　Fig.1 Typical topology of parallel system of converters

　　1.3 暂态交互模型及验证

　　本文以2台变换器并联系统为例，分析变换器间暂态交互对并联系统稳定性的影响。以变换器和理想电源并网母线作为端口，经星形-三角形变换消去PCC，得到变换后的等值电路如图2所示。图中：(delta_1)、(delta_2)、(delta_g)分别为变换器1、变换器2、理想电源的功角;(Z_{1g})、(Z_{2g})、(Z_{12})分别为星形-三角形变换后变换器1与理想电源间、变换器2与理想电源间、变换器1与变换器2间的阻抗。并联变换器接入系统可视为3机暂态相互作用系统，故障下，任意1台设备均与其他2台设备存在暂态交互，该交互作用影响变换器虚拟转子加减速动态，继而又对三者交互产生影响。下文将对此进行建模分析。

　　图2 消去PCC的等值电路

　　Fig.2 Equivalent circuit after eliminating PCC

　　假定所有阻抗均为感性，分别为变换器1与理想电源间、变换器2与理想电源间、变换器1与变换器2间的电抗。系统节点电压方程为：

　　式中：(Y_{ii})为变换器的自导纳，其中，(i=1,2);(Y_{ij})为变换器间的互导纳，(j=1,2);(Y_{g1})和(Y_{1g})为变换器1与理想电源间的互导纳;(Y_{g2})和(Y_{2g})为变换器2与理想电源间的互导纳;(Y_{gg})为理想电源的自导纳;(dot{I}_1)、(dot{I}_2)、(dot{I}_g)分别为变换器1、变换器2、理想电源输出的电流相量;(dot{E}_1)、(dot{E}_2)、(dot{E}_g)分别为变换器1、变换器2、理想电源的内电势相量。

　　根据短路故障后变换器是否触发限流控制分为以下3种情况：

　　- 情况1：2台变换器均未触发限流控制;

　　- 情况2：仅1台变换器触发限流控制;

　　- 情况3：2台变换器均触发限流控制。

　　对于2台变换器均未触发限流控制的情况，求解式(1)得到变换器1和2的电磁功率分别为：

　　式中：(I_1)为限流变换器1的输出电流。

　　变换器输出电磁功率包含了变换器间以及变换器与理想电源间的交互功率。以仅1台变换器触发限流控制为例，式(4)中，(E_1E_gY_{1g}sin(delta_1-delta_g))表示变换器1通过支路(Y_{1g})与理想电源交互功率，(E_1E_gY_{12}Y_{22}^{-1}Y_{2g}sin(delta_1-delta_g))表示变换器1经(Y_{12})、(Y_{2g})支路与理想电源交互功率，以上2项体现了变换器1与理想电源间的暂态交互作用;(E_1Y_{12}Y_{22}^{-1}I_2cos[delta_1-(delta_2+varphi)])表示变换器1与处于限流状态的变换器2间的交互功率，该交互功率也存在于式(5)中，并且符号相反。式(5)中，(Y_{22}^{-1}Y_{2g}I_2E_gcos[(delta_2+varphi)-delta_g])表示变换器2经支路(Y_{2g})与理想电源交互功率。可以看出，变换器1、变换器2和理想电源三者间存在暂态功率交互，在支路参数一定的情况下，三者交互作用大小与电压幅值、相位、限流相位以及限流幅值有关。

　　进一步的，考虑到暂态同步稳定分析的时间尺度通常为百毫秒级以上，可以忽略电流内环控制动态和电磁暂态过程，仅考虑虚拟转子运动过程。2台构网型变换器转子运动方程为：

　　式中：(Deltaomega_1)和(Deltaomega_2)分别为变换器1和2的虚拟角速度变化量;(J_1)和(J_2)分别为变换器1和2的虚拟惯量，采用惯性时间常数表示，单位为s;(D_1)和(D_2)分别为变换器1和2的阻尼系数;(P_{1ref})和(P_{2ref})分别为变换器1和2的参考有功功率。

　　式(8)与式(2)一式(7)共同构成构网型变换器并联系统暂态交互模型，其框图如图3所示。图中：(omega_0)为基准转速;(omega_1)和(omega_2)分别为变换器1和2的虚拟转速;(Delta P_{12})为变换器间交互功率;(s)为微分算子。

　　图3 变换器并联系统暂态交互模型

　　Fig.3 Transient interaction model of parallel system of converters

　　2 暂态同步稳定性分析

　　电网短路故障持续期间及恢复过程中，并联运行的构网型变换器与系统间存在复杂的暂态交互，该交互过程影响多机相对运动。同时，又受到多机相对运动的影响。本章重点讨论多机暂态交互作用对变换器暂态同步稳定的影响机理，进而揭示变换器暂态同步稳定和失稳机制。

　　2.1 暂态交互能量作用机理

　　根据第1章构建的暂态交互模型，可推导多变换器暂态能量转化特性，对式(8)进行积分得到：

　　式中：(J)为采用惯性时间常数表示的惯量;(Deltaomega)为虚拟转速偏差;(delta_0)为扰动起始时刻变换器虚拟功角;(delta_t)为(t)时刻虚拟功角;(Delta E_K)为虚拟转子动能变化量;(P_e)和(P_{ref})分别为电磁功率和有功功率参考值;(Delta E_V)为虚拟转子势能变化量，由变换器与系统交互能量(Delta E_{cs})和变换器间交互能量(Delta E_{12})组成;(D)为阻尼系数;(Delta E_D)为虚拟阻尼的耗散能量变化量。不难看出，在功角运动过程中，(Delta E_K)和(Delta E_V)呈现相互转换特性，阻尼在能量转换过程中能够消耗过剩的动能或势能，促使功角收敛至平衡点。

　　设(P_{12})为变换器1流向变换器2的有功功率，则(Delta P_{12}=P_{12}-P_{12,0})为变换器1流向变换器2有功功率相对初始值的变化，本文定义为变换器间交互功率，其中，(P_{12,0})为故障发生前变换器1流向变换器2的有功功率。故障发生时刻至功角最大值时刻变换器间暂态交互能量表示为：

　　式(10)中等号右边第1项(Delta E_{12}')是故障期间变换器间暂态交互能量，该值影响故障期间虚拟动能最大值(Delta E_{K,max});第2项(Delta E_{12}'')是故障清除时刻至功角最大值时刻变换器间暂态交互能量，该值影响变换器可供转化的最大势能(Delta E_{V,max})。故障期间变换器暂态交互对变换器功角曲线影响通过图4说明。图中：SEP和UEP分别表示稳定平衡点和不稳定平衡点。变换器间暂态交互能量在故障期间、恢复过程中均对暂态稳定性产生影响。对于换流器并联接入理想电源系统，短路故障下变换器虚拟转子加速，虚拟功角将超前理想电源。故障消失后，由于虚拟转子惯量作用，功角将继续运动直至达到(delta_{max})，故(delta_0<delta_c<delta_{max})。结合式(10)可知，(Delta E_{12}')与(Delta E_{12}'')的正负仅与(Delta P_{12})的正负相关，而(Delta P_{12})的正负与变换器相对功角差变化相关，下节将对此进行说明。当(Delta E_{12}'>0)时，故障期间变换器1向变换器2提供交互能量，变换器1加速动能减少，有利于变换器1暂态稳定;当(Delta E_{12}''>0)时，故障后变换器1向变换器2提供交互能量，变换器1可转化势能增加，同样有利于变换器1暂态稳定;反之，则不利于暂态稳定。

　　图4 暂态交互对变换器功角曲线的影响

　　Fig.4 Influence of transient interaction on power angle curve of converter

　　综上，并联系统受扰后暂态交互能量在变换器间流动，通过增加或减少虚拟动能或势能的方式对变换器暂态稳定性产生影响。

　　2.2 暂态交互能量的牵引机制

　　假定故障能够及时切除，变换器间相对功角不超过90°，变换器机端电压能够瞬间跟踪指令值。在上述假定条件下进行分析。根据两机并联暂态交互模型，对于故障后2台变换器均不限流的情况，由式(1)可知，变换器1流向变换器2的功率为(E_1E_2Y_{12}sin(delta_1-delta_2))，变换器间交互功率为(Delta P_{12}=E_1E_2Y_{12}[sin(delta_1-delta_2)-sindelta_{12,0}])，其中，(delta_{12,0})为故障前变换器1与变换器2的功角差。对于2台变换器均限流的情况，变换器1流向变换器2的功率为(Y_{12}(Y_{22}Y_{11}+Y_{12}Y_{12})^{-1}I_2I_1sin(delta_1-delta_2))，变换器间交互功率为(Delta P_{12}=Y_{12}(Y_{22}Y_{11}+Y_{12}Y_{12})^{-1}I_2I_1[sin(delta_1-delta_2)-sindelta_{12,0}])。由于(E_1)、(E_2)、(Y_{12})、(Y_{11})、(Y_{22})、(I_1)、(I_2)均为正值，不难得出，变换器间交互功率(Delta P_{12})的方向仅与(sin(delta_1-delta_2)-sindelta_{12,0})的正负有关，即故障后功角差相对于故障前初值的变化仅与(Deltasin(delta_1-delta_2))正负有关。若变换器1和2的功角差变化量(Delta(delta_1-delta_2)>0)，即故障后变换器1功角加速更多，稳定性更差，则(Deltasin(delta_1-delta_2)>0)、(Delta P_{12}>0)、(Delta E_{12}>0)，变换器1向变换器2提供交互能量，提高了稳定性更差的变换器1的稳定性，同时，由于变换器2吸收了变换器提供的交互能量，降低了稳定性更好的变换器2的稳定性;反之，(Delta E_{12}<0)，变换器2向变换器1提供交互能量，同样提高了稳定性更差的变换器2的稳定性，降低了稳定性更好的变换器1的稳定性。暂态能量交互作用使得两者稳定性趋近一致。

　　对于故障后仅变换器2限流的情况，(Delta P_{12})方向主要由(-cos[delta_1-(delta_2+varphi)])决定，其中，(varphi)与限流策略有关。1)若限流策略为d轴优先，即(varphi=0^circ)，故障发生后，变换器2进入限流状态，功角加速更多，稳定性更差，(cos(delta_1-delta_2)>0)、(Delta P_{12}<0)、(Delta E_{12}<0)，稳定性较差的限流变换器向不限流变换器提供交互能量，降低了稳定性较好的不限流变换器的稳定性，提升了稳定性较差的限流变换器的稳定性，两者稳定性趋近一致。2)若限流策略为q轴优先，即(varphi=90^circ)，故障发生后，变换器2进入限流状态，功角加速更多，稳定性更差，(sin(delta_1-delta_2)<0)，(Delta P_{12}>0)、(Delta E_{12}>0)，稳定性较好的不限流变换器向限流变换器提供交互能量，提升了稳定性较好的不限流变换器的稳定性，降低了稳定性较差的限流变换器的稳定性;进一步地，故障清除后，由于惯性，限流变换器角度将继续增加，若临近失稳依然处于限流状态或由不限流再次进入限流状态，则限流变换器将加速失稳。

　　由以上分析不难看出，变换器间暂态交互能量对并联运行变换器稳定性可能产生2种影响：1)变换器稳定性趋近一致，功角变化快的变换器向功角变化慢的变换器提供暂态能量，使得功角变化快的变换器角度增加放缓，功角变化慢的变换器角度增加加快，最终稳定性趋近一致;2)稳定性较差的变换器加速失稳，功角变化慢的变换器向功角变化快的变换器提供暂态能量，使得功角变化快的变换器角度增加加快，功角变化慢的变换器角度增加放缓，最终稳定性较差的变换器将加速失稳。以上两方面体现出暂态交互能量作用下的功角牵引机制。该机制可能使得单机运行时暂态失稳的变换器在并联系统中稳定运行，也可能使得单机运行稳定的变换器在并联系统中失去稳定，增加了并联系统短路故障下暂态同步稳定的不确定性。

　　从变换器暂态交互模型可以看出，变换器间耦合功率除受功角影响外，还与端电压、是否限流以及限流策略相关。因此，交互功率不一定单向流动，可能在变换器间循环往复、正负交替出现。暂态交互能量也在变换器动能和势能相互转化的过程中发挥作用，影响变换器暂态稳定性。因此，首摆相继失稳的2台变换器也可能在后续摆次中由于暂态交互作用而出现再同步现象。变换器间暂态交互引起的再同步功角曲线如附录B图B1所示。为分析方便，假定初始状态(delta_1<delta_2)，虚线为(Delta P_{12})对变换器1电磁功率的影响，A、C点为不稳定平衡点，B点为稳定平衡点。故障发生后，假定(Delta(delta_1-delta_2)<0)，则(Delta P_{12}<0)、变换器1虚拟动能增加，如图中红色区域所示，故障清除后，(Delta P_{12})仍然小于0、(delta_1)继续加速，越过E点后(Delta(delta_1-delta_2)>0)，(Delta P_{12}>0)、(Delta P_{12})增加部分势能如图中蓝色区域所示。若进入某个失步周期时，变换器1势能恰好能够将动能全部转化，则变换器1将实现再同步[20]。

　　3 并联系统的稳定域

　　3.1 稳定域构建

　　由于构网型变换器并联系统等效方程中含有能量耗散的阻尼项，基于能量函数求解暂态稳定域的直接方法都存在一定程度的保守性。相比之下，通过微分几何流形稳定性理论，可以获得一个保守性较小的稳定区域。根据流形稳定性理论[31]，动力学系统中，不稳定平衡点的稳定流形构成稳定域边界，并将相平面划分了2个区域，即稳定区域和不稳定区域，远离不稳定平衡点的流形称为不稳定流形，逼近不稳定平衡点的流形称为稳定流形。通过判断故障后运行点位于稳定域内或外，可得到故障后变换器的稳定状态，稳定域面积的大小代表了变换器稳定性的强弱。本文即利用数值方法求取并联变换器稳定域，具体做法是对不稳定平衡点在稳定流形方向求反时间积分。

　　2台变换器并联系统包含(delta_1)、(delta_2)、(Deltaomega_1)、(Deltaomega_2)这4个状态变量，这些状态变量构成的四维空间不利于观察和分析稳定域边界。由前文分析可知，2台构网型变换器间暂态交互能量的功角牵引机制作用，促使2台变换器稳定性趋近一致或稳定性较差变换器加速失稳。因此，同一场站内并联运行的变换器间相对失稳不是研究重点，更应关注的是变换器相对外部系统的稳定性问题。由此，采用向单变换器(Deltaomega-delta)构成的二维平面投影方式对并联系统进行状态变量降维，得到任一变换器的运动相图，通过投影方式得到的变换器运动轨迹即反映了变换器暂态交互对稳定性的影响。

　　故障消失后系统恢复过程中，变换器暂态限流环节会在动作和不动作之间切换，故需计及构网型变换器限流切换控制构建并联系统稳定域。需要注意的是，根据2台变换器故障后是否限流，存在以下4种情况：均不限流、仅变换器1限流、仅变换器2限流、均限流。因此，通过假定故障后限流器运行状态可以得到并联系统在一个周期内的4个UEP。但假定的限流状态必须与实际的电流值吻合才是合理的。因此，分别计算各UEP变换器输出电流，判断变换器实际所属限流状态，进而剔除不合理的UEP，保留合理的UEP。在UEP进行反时间积分，积分过程中逐点判断变换器所处的运行状态，根据运行状态对暂态交互模型进行模型切换，进而得到计及切换控制的稳定域。下文结合实际计算结果进行说明。

　　为分析简便，假定2台变换器参数完全相同，限流幅值均为1.5 p.u.，即变换器间无暂态交互，2台变换器限流状态相同。图5为通过投影降维方式得到的计及限流切换的变换器稳定域。图中：(SEP_1)和(SEP_2)分别为不限流和限流变换器稳定平衡点;(UEP_1)和(UEP_2)分别为限流变换器的不稳定平衡点;(UEP_3)为不限流变换器的不稳定平衡点;A、(A')、(B')为限流与不限流状态的切换点。通过在不稳定平衡点进行反时间积分，可以得到一个周期内变换器限流稳定域和不限流稳定域，分别如图5中红色曲线包围的S1区域和青色曲线包围的S2区域所示。计及切换控制，如图5中橙色箭头所示，从限流状态(UEP_2)出发反时间积分，首先到达青色和红色曲线的交点，但因为该点仍然位于限流区域，所以会沿着限流的轨迹红色曲线继续反时间运动到达A点，在A点左侧区域，变换器电流不越限，切换到不限流轨迹(蓝色曲线)继续反时间积分，到达(A')点，再次切换到限流轨迹(褐色曲线)，直到达到(B')点，此时电流不再越限，再次切换到不限流轨迹(绿色曲线)继续反时间积分。由此得到计及限流切换的系统稳定域如图5中灰色区域所示。故障后系统稳定运行点若落在灰色区域内，则最终会运动到(SEP_1)。可以看出，计及限流切换后，系统稳定域边界由不同轨迹线构成，与限流稳定域与不限流稳定域存在显著差别。下节将利用本文提出的并联系统稳定域构建方法分析计及暂态交互后变换器运行状态及参数对暂态同步稳定性的影响。计及限流切换的构网型并联系统稳定域构建步骤如附录B图B2所示。

　　图5 计及限流切换的并联系统稳定域

　　Fig.5 Stability domain of parallel system considering current limiting switching

　　3.2 稳定性影响因素分析

　　由变换器暂态交互模型可知，暂态交互能量大小和方向受变换器运行点、控制参数、并网阻抗、限流值大小等因素影响，进而影响并联系统稳定性。本节以故障后仅1台变换器限流为例，利用稳定域方法分析限流变换器运行状态及参数变化对不限流变换器稳定性的影响。设置变换器2电流限幅值为1.5 p.u.，限流策略分别考虑d轴优先和q轴优先，变换器1不设电流限幅。下文给出的是变换器1稳定域的变化。需要说明的是，在工程应用中，应分别作出所有变换器的稳定域，进而评估并联系统整体的稳定性。

　　3.2.1 初始运行点的影响

　　设置场景1中(P_{1ref}=P_{2ref}=0.5) p.u.，对比场景2中(P_{1ref}=0.5) p.u.、(P_{2ref}=1.0) p.u.，其余参数相同。对于场景1，变换器间不存在交互能量;对于场景2，故障后限流变换器2向不限流变换器1提供交互能量，随变换器2初始出力增加，稳定性更差，故障后功角加速更多，(delta_1-delta_2)绝对值更大，(cos(delta_1-delta_2))更小，故暂态交互能量更小，不限流变换器稳定域扩大，稳定性提升。q轴优先策略下，场景2不限流变换器1向限流变换器2提供交互能量，随变换器2初始出力增加，稳定性更差，故障后功角加速更多，(delta_1-delta_2)为负，且绝对值更大，(sin(delta_1-delta_2))更小，故暂态交互能量减小，不限流变换器稳定域缩小，稳定性降低，图6(a)和(b)所示稳定域计算结果与上述分析结论一致。

　　3.2.2 并网阻抗的影响

　　(P_{1ref}=P_{2ref}=0.5) p.u.，设置场景1中变换器并网阻抗(X_1=X_2=0.05) p.u.，对比场景2中(X_1=0.05) p.u.、(X_2=0.07) p.u.，其余参数相同。对于场景1，变换器间不存在交互能量;对于场景2，故障后限流变换器2向不限流变换器1提供交互能量，随着变换器2并网阻抗增加，稳定性更差，(delta_1-delta_2)绝对值更大，(cos(delta_1-delta_2))更小，故暂态交互能量更小，不限流变换器稳定域扩大，稳定性提升。q轴优先策略下，场景2不限流变换器1向限流变换器2提供交互能量，随变换器2初始出力增加，稳定性更差，故障后功角加速更多，(delta_1-delta_2)为负，且绝对值更大，(sin(delta_1-delta_2))更小，故暂态交互能量减小，不限流变换器稳定域缩小，稳定性降低。图6(c)和(d)所示稳定域计算结果与上述分析结论一致。

　　值得注意的是，对于实际的新能源场站而言，站内阻抗分布不均，实际上不同位置变换器的并网阻抗不同，这种差异虽不会导致变换器间相对失稳，但相对功角产生的暂态交互能量将对变换器暂态同步稳定性产生影响。限流变换器的并网阻抗越大，故障后其稳定性越差，但将使得不限流变换器的稳定性越好，这其实也体现了前文所提功角牵引机制的第2种情形。

　　3.2.3 变换器惯量参数的影响

　　(P_{1ref}=P_{2ref}=0.5) p.u.，设置场景1中(J_1=J_2=5) s，对比场景2中(J_1=5) s、(J_2=8) s，其余参数相同。对于场景1，变换器间不存在交互能量;对于场景2，变换器2惯量增加，故障后加速更慢，即(delta_1-delta_2>0)，d轴优先策略下，(cos(delta_1-delta_2)>0)、(Delta P_{12}<0)、(Delta E_{12}<0)，故障后限流变换器2向不限流变换器1提供交互能量，随着惯量增加，(cos(delta_1-delta_2))更小，故暂态交互能量更小，不限流变换器稳定域扩大，稳定性提升。q轴优先策略下，场景2有(delta_1-delta_2)为正，且随惯量增加，(delta_1-delta_2)的绝对值更大，(sin(delta_1-delta_2))更大，有(sin(delta_1-delta_2)>0)、(Delta P_{12}<0)、(Delta E_{12}<0)，故障后限流变换器2向不限流变换器1提供交互能量更小，不限流变换器稳定域缩小，稳定性下降。图6(e)和(f)所示稳定域计算结果与上述分析结论一致。

　　图6 运行状态及参数对稳定域的影响

　　Fig.6 Influence of operating status and parameters on stability domain

　　综上所述，限流变换器初始运行点、并网阻抗、控制参数等因素对不限流变换器暂态稳定性产生影响。从上述分析看出，d轴电流优先策略下，限流变换器初始运行功率越高，并网阻抗越大，惯量参数越大，越有利于不限流变换器的暂态稳定性。q轴电流优先策略则相反。

　　4 仿真验证

　　为了验证上述理论分析的正确性，基于PSCAD/EMTDC构建了如图1所示的2台构网型变换器并联系统时域仿真模型。仿真参数如附录C表C1所示。本文通过电网电压的对称跌落模拟电网发生三相对称短路故障，故障设置为3.0 s时电网电压跌落至0.05 p.u.。

　　4.1 暂态交互模型有效性验证

　　对构网型变换器并联系统电磁暂态详细模型与本文构建的暂态交互模型进行仿真对比。3.0 s时系统侧发生三相短路故障，3.5 s故障消失。变换器1不设置电流限幅，变换器2限流策略为d轴优先，限幅值为1.5 p.u.。附录C图C1给出了变换器1、变换器2以及变换器间交互有功功率曲线。3.0 s故障发生后，变换器2切换至限流控制模式，交互功率由变换器2流向变换器1，3.5 s故障消失后，系统电压迅速恢复，变换器2仍处于限流状态，直到3.83 s，变换器2从限流状态恢复。从图中可以看出，仅在故障发生、消失以及限流切换的数十毫秒内存在差别，其余时段详细模型计算结果与交互模型完全吻合，满足百毫秒时间尺度暂态同步稳定问题的研究需要。

　　4.2 暂态交互能量的牵引机制验证

　　4.2.1 同步稳定

　　设置(P_{1ref}=1.0) p.u.、(P_{2ref}=0.5) p.u.，2台变换器均不限流。3.0 s时发生短路故障，持续时间为0.19 s，2台变换器单独运行和并联运行时的虚拟功角变化分别如附录C图C2(a)和(b)所示。可以看出，2台变换器单独运行时，变换器1失稳，变换器2稳定。2台变换器并联运行时，暂态能量由变换器1流向变换器2，如附录C图C3所示。暂态能量交互提升了变换器1的稳定性，变换器2功角首摆幅度增加，但扰动后2台变换器均趋于稳定，并联系统暂态稳定性提高。

　　4.2.2 相继失稳

　　设置(P_{1ref}=1.0) p.u.、(P_{2ref}=0.8) p.u.，2台变换器均不限流。3.0 s时发生短路故障，持续时间为0.24 s，2台变换器单独运行和并联运行时的虚拟功角变化分别如附录C图C4(a)和(b)所示。可以看出，2台变换器单独运行时，变换器1失稳，变换器2稳定。2台变换器并联运行时，暂态能量由变换器1流向变换器2，并且随时间持续增加，暂态交互能量逐渐增大，如附录C图C5所示。暂态能量交互降低了变换器2的稳定性，扰动后2台变换器相继失稳，并联系统暂态稳定性下降。

　　4.2.3 再同步

　　设置(P_{1ref}=1.0) p.u.、(P_{2ref}=0.5) p.u.，2台变换器均不限流。3.0 s时发生短路故障，持续时间为0.29 s，2台变换器单独运行和并联运行时的虚拟功角变化分别如附录C图C6(a)和(b)所示。可以看出，2台变换器单独运行时，变换器1失稳，变换器2稳定。2台变换器并联运行时，暂态能量由变换器1流向变换器2，如附录C图C7所示。其中，3.00~3.94 s期间，变换器1流向变换器2暂态能量增加，变换器2随变换器1首摆失稳，3.94~4.31 s期间，变换器1流向变换器2的暂态能量减少，变换器2和变换器1的加速动能被势能完全转化，变换器在第2摆恢复稳定，实现了再同步。

　　4.2.4 加速失稳

　　设置(P_{1ref}=1.0) p.u.、(P_{2ref}=1.8) p.u.，变换器2限流值为1.5 p.u.、q轴优先。3.0 s时发生短路故障，持续时间为0.22 s，2台变换器单独运行和并联运行时的虚拟功角变化分别如图7(a)和(b)所示。可以看出，2台变换器单独运行时，2台变换器均稳定，并联运行时变换器2失稳。图7(c)为暂态交互能量和变换器2限流环节动作信号，图7(d)为变换器2输出电流曲线。从图中可以看出，3.0 s故障发生后，变换器2限流环节动作，交互能量由不限流变换器1流向限流变换器2，导致变换器2功角增加更为迅速;故障消失后，变换器2仍处于限流状态，功角持续加大，期间变换器2相对系统失稳。可见，变换器间交互的暂态能量导致了限流变换器加速失稳。

　　图7 变换器2加速失稳仿真结果

　　Fig.7 Simulation results of accelerated instability of converter 2

　　4.3 并联系统稳定域验证

　　4.3.1 不计限流切换

　　通过计算临近稳定边界的相轨迹验证稳定域的正确性。设置(P_{1ref}=1.0) p.u.、(P_{2ref}=0.5) p.u.，3.0 s时发生短路故障，通过不断延长故障切除时间，相轨迹将逐渐远离稳定域，持续时间为0.28 s和0.30 s的相轨迹及稳定域如附录C图C8所示。图中：SEP为变换器1初始运行点，发生三相接地故障后，系统运行状态从SEP开始沿绿色曲线移动。若在0.28 s切除故障，则系统状态由稳定域内(B_1)点沿绿色曲线重新回到SEP;若0.30 s后切除故障，则系统状态由稳定域外(B_2)点沿红色曲线失稳。变换器1稳定域与仿真计算结果吻合。

　　4.3.2 计及限流切换

　　设置(P_{1ref}=1.0) p.u.、(P_{2ref}=0.5) p.u.，变换器限流值均为1.5 p.u.。3.0 s时发生短路故障，通过不断延长故障切除时间，相轨迹将逐渐远离稳定域，持续时间为0.22 s和0.23 s的相轨迹及稳定域如图8所示。图中：灰色区域即为稳定域，其边界轨迹线含义与图5相同。发生三相接地故障后，系统运行状态从SEP开始沿绿色曲线移动。若在0.22 s切除故障，则系统状态由稳定域内(B_1)点沿绿色曲线重新回到平衡点，若0.23 s后切除故障，则系统状态由稳定域外(B_2)点沿紫色曲线失稳。考虑限流切换后的变换器1稳定域与仿真计算结果吻合。

　　图8 系统运行相轨迹与稳定域

　　Fig.8 Phase trajectory and stability domain of system operation

　　4.4 稳定性影响因素验证

　　以仅1台变换器限流情况为例进行稳定性影响因素验证。变换器2限流值为1.5 p.u.，限流策略分别考虑d轴优先和q轴优先。变换器1设置为不限流。

　　4.4.1 初始运行点的影响验证

　　设置(P_{1ref}=0.5) p.u.，(P_{2ref})分别设置为0.5、0.8、1.0 p.u.。3.0 s时发生三相接地短路故障，故障持续时间为0.1 s。附录C图C9给出了d轴优先策略下，变换器1虚拟功角变化和暂态交互能量变化。d轴优先策略下，交互能量由限流变换器2流向不限流变换器1。随着变换器2出力增加，暂态交互能量减小，有利于不限流变换器的稳定性。

　　附录C图C10给出了q轴优先策略下，变换器1虚拟功角变化和暂态交互能量变化。q轴优先策略下，交互能量由不限流变换器1流向限流变换器2。随着变换器2出力增加，暂态交互能量减小，不利于不限流变换器稳定性。

　　附录C图C11为q轴优先策略下变换器间交互能量与变换器2限流动作信号。从图中可以看出，仅故障期间限流环节动作，该时段交互能量由不限流变换器1流向限流变换器2，有利于变换器的稳定;故障消失后，限流环节不再动作，交互能量开始反向流动，不利于变换器1的稳定。与2.2节分析结论一致。

　　4.4.2 并网阻抗的影响验证

　　本节验证限流变换器并网阻抗变化对不限流变换器稳定性的影响。设置(P_{1ref}=P_{2ref}=1.0) p.u.，(X_1=0.05) p.u.，分别设置(X_2)为0.05、0.10、0.15 p.u.。3.0 s时发生三相接地短路故障，故障持续时间为0.1 s。附录C图C12给出了d轴优先策略下变换器1虚拟功角变化和暂态交互能量变化。可以看出，d轴优先策略下，随着变换器2阻抗增加，扰动后由变换器2流向变换器1的交互能量减小，变换器1的暂态稳定性提高。q轴优先策略下则相反，如附录C图C13所示。

　　4.4.3 变换器惯量参数的影响验证

　　设置(P_{1ref}=P_{2ref}=1.0) p.u.，(J_1=5) s，分别设置(J_2)为5、8、10 s。3.0 s时发生三相接地短路故障，故障持续时间为0.1 s。d轴优先策略下，扰动后随着变换器2惯量增加，由变换器2流向变换器1的暂态交互能量减少，变换器1暂态稳定性得到提高，如附录C图C14所示。q轴优先策略则相反，如附录C图C15所示。

　　上述仿真结果与前文基于稳定域的运行状态及参数对暂态同步稳定性影响的分析结果一致。

　　5 实验验证

　　为进一步验证本文所提暂态稳定方法以及参数影响分析的正确性，基于RTDS平台构建了包含2台构网型变换器控制器的硬件在环实验平台，如附录D图D1所示，该实验平台由RTDS实时仿真器、2台构网型变换器控制器、I/O板卡构成。电网一次系统、变换器主电路以及大扰动故障均通过RTDS实时仿真器模拟，变换器控制器输出脉冲信号返回至RTDS。系统参数如附录C表C1所示。变换器1不设置电流限幅，变换器2电流限幅策略为d轴优先，限幅值为1.5 p.u.。故障设置为10 s时电网电压跌落至0.05 p.u.，持续时间为0.2 s。通过调整变换器1并网阻抗和惯量参数，使得2台变换器间交互能量发生变化，进一步对比参数调整前后2台变换器功角曲线以及稳定性变化情况，验证本文分析结论。

　　5.1 并网阻抗影响实验

　　参数调整前的实验波形如图9所示。图中：从上到下依次为参数调整前变换器1功角曲线、变换器2功角曲线以及变换器2限流动作信号。可以看出，故障后变换器2触发限流动作，功角增加，d轴优先策略使得交互能量由变换器1流向变换器2，变换器2加速失稳。

　　图9 参数调整前的实验波形

　　Fig.9 Experimental waveforms before parameter adjustment

　　增加变换器1并网阻抗，设置为(X_1)为0.08 p.u.。参数调整后，故障下变换器1功角增加变快，降低了由变换器1流向变换器2的交互能量，虽然恶化了不限流变换器1的稳定性，但是提升了限流变换器2的稳定性，最终2台变换器相对系统均暂态稳定，如图10所示。实验结果与前文理论分析结论一致。

　　图10 阻抗参数调整后的实验波形

　　Fig.10 Experimental waveforms after impedance parameter adjustment

　　5.2 变换器惯量参数影响实验

　　仍然采用附录C表C1所示系统参数，实验波形见图9。减小变换器1惯量参数，使得故障后变换器1功角增加变快，同样降低了由变换器1流向变换器2的交互能量，恶化了不限流变换器1的稳定性，但是提升了限流变换器2的稳定性，2台变换器相对系统也暂态稳定，如图11所示。实验结果与前文理论分析结论一致。

　　图11 惯量参数调整后的实验波形

　　Fig.11 Experimental waveforms after inertia parameter adjustment

　　6 结语

　　本文通过建立构网型变换器并联运行暂态交互模型，揭示了暂态交互能量对变换器稳定性的影响机理，发现了暂态交互能量的功角牵引机制对变换器稳定性的2种影响，通过构建计及限流切换的构网型变换器并联系统稳定域，分析了运行状态和参数变化对稳定性的影响规律，并进行了仿真和实验验证。主要结论如下：

　　1) 短路故障下，构网型变换器间存在交互能量的流动，并对变换器暂态稳定性产生影响。交互能量的大小和流动方向主要由变换器相对功角以及限流策略决定。

　　2) 由于暂态交互能量的影响，存在单机运行时暂态失稳的变换器在并联系统中稳定运行，或单机运行稳定的变换器在并联系统中失去稳定，或首摆失稳后再同步的现象，增加了并联系统短路故障下暂态同步稳定的不确定性。

　　3) 发现交互能量作用下变换器间存在功角牵引机制，该机制将促使多变换器稳定性趋近一致或致使稳定性较差的变换器加速失稳。

　　4) 提出的计及限流切换的并联系统稳定域降维构建方法能够直观反映运行状态及参数变化对暂态稳定性的影响，可以为并联系统运行状态调整及控制参数优化提供指导。采用d轴优先的电流限幅策略，限流变换器初始运行功率越高，并网阻抗越大，惯量参数越大，越有利于不限流变换器的暂态稳定性。q轴优先的电流限幅策略则相反。

　　本文以两构网型变换器并联接入理想电源系统为研究对象，分析结论适用于故障下变换器相位超前于理想电源的场景。需要注意的是，在多机系统中，尤其是多构网型变换器与同步发电机混联系统中，其暂态过程更为复杂，变换器与同步发电机相位的超前滞后关系可能导致分析结论完全相反，需要进一步研究。同时，如何协同控制多台构网型变换器提升并联系统暂态同步稳定性也将是下一步研究的重点。

　　参考文献

　　[1] 国家能源局发布2023年全国电力工业统计数据[EB/OL]. (2024-01-16)[2024-04-20]. https://www.nea.gov.cn/2024-01/26/c_1310762246.htm. National Energy Administration releases statistical data on the national power industry for 2023[EB/OL]. (2024-01-16)[2024-04-20]. https://www.nea.gov.cn/2024-01/26/c_1310762246.htm.

　　[2] 新型电力系统发展蓝皮书[M]. 北京: 中国电力出版社, 2023. Blue book of new power system development[M]. Beijing: China Electric Power Press, 2023.

　　[3] 孙华东, 徐式蕴, 许涛, 等. 电力系统安全稳定性的定义与分类探析[J]. 中国电机工程学报, 2022, 42(21): 7796-7809. SUN Huadong, XU Shiyun, XU Tao, et al. Research on definition and classification of power system security and stability[J]. Proceedings of the CSEE, 2022, 42(21): 7796-7809.

　　[4] 熊佳旺, 孔力, 叶华, 等. 弱电网中锁相环型并网变换器非线性暂态稳定解析分析[J]. 电力系统自动化, 2022, 46(24): 76-84. XIONG Jiawang, KONG Li, YE Hua, et al. Analytical analysis on nonlinear transient stability of phase-locked loop type grid connected converter in weak power grid[J]. Automation of Electric Power Systems, 2022, 46(24): 76-84.

　　[5] 许诘翊, 刘威, 刘树, 等. 电力系统变流器构网控制技术的现状与发展趋势[J]. 电网技术, 2022, 46(9): 3586-3595. XU Jieyi, LIU Wei, LIU Shu, et al. Current state and development trends of power system converter grid-forming control technology[J]. Power System Technology, 2022, 46(9): 3586-3595.

　　[6] ROSSO R, WANG X, LISERRE M, et al. Grid-forming converters: control approaches, grid-synchronization, and future trends-a review[J]. IEEE Open Journal of Industry Applications, 2021, 2: 93-109.

　　[7] ZHANG H B, XIANG W, LIN W X, et al. Grid forming converters in renewable energy sources dominated power grid: control strategy, stability, application, and challenges[J]. Journal of Modern Power Systems and Clean Energy, 2021, 9(6): 1239-1256.

　　[8] WU H, RUAN X B, YANG D S, et al. Small-signal modeling and parameters design for virtual synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4292-4303.

　　[9] ROSSO R, ENGELKEN S, LISERRE M. On the implementation of an FRT strategy for grid-forming converters under symmetrical and asymmetrical grid faults[J]. IEEE Transactions on Industry Applications, 2021, 57(5): 4385-4397.

　　[10] 王盼宝, 王鹏, 李珅光, 等. 电网故障下构网型逆变器动态限流控制策略[J]. 高电压技术, 2022, 48(10): 3829-3837. WANG Panbao, WANG Peng, LI Shenguang, et al. Dynamic current-limiting control strategy of grid-forming inverter under grid faults[J]. High Voltage Engineering, 2022, 48(10): 3829-3837.

　　[11] WU H, WANG X F. Design-oriented transient stability analysis of grid-connected converters with power synchronization control[J]. IEEE Transactions on Industrial Electronics, 2019, 66(8): 6473-6482.

　　[12] HU P F, JIANG W T, YU Y X, et al. Transient stability improvement of grid-forming voltage source converters considering current limitation[J]. Sustainable Energy Technologies and Assessments, 2022, 54: 102839.

　　[13] LIU T, WANG X F. Transient stability of single-loop voltage-magnitude controlled grid-forming converters[J]. IEEE Transactions on Power Electronics, 2021, 36(6): 6158-6162.

　　[14] ROKROK E, QORIA T, BRUYERE A, et al. Transient stability assessment and enhancement of grid-forming converters embedding current reference saturation as current limiting strategy[J]. IEEE Transactions on Power Systems, 2022, 37(2): 1519-1531.

　　[15] 蒙昌鑫, 王延旭, 王威儒, 等. 跟网/构网控制交互下换流器中频特性分析及振荡抑制[J/OL]. 电力系统自动化[2024-09-27]. https://kns.cnki.net/kcms/detail/32.1180.TP.20240920.1148.003.html. MENG Changxin, WANG Yanxu, WANG Weiru, et al. Medium-frequency characteristic analysis and oscillation suppression of converter with interaction between grid-forming and grid-following control[J/OL]. Automation of Electric Power Systems[2024-09-27]. https://kns.cnki.net/kcms/detail/32.1180.TP.20240920.1148.003.html.

　　[16] ZHAO J T, HUANG M, ZHA X M. Transient stability analysis of grid-connected VSIs via PLL interaction[C]// 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), November 4-7, 2018, Shenzhen, China.

　　[17] QORIA T, GRUSON F, COLAS F, et al. Current limiting algorithms and transient stability analysis of grid-forming VSCs[J]. Electric Power Systems Research, 2020, 189: 106726.

　　[18] 刘雨昕, 彭克, 赵子达, 等. 多虚拟同步发电机并联系统功率低频振荡机理分析[J]. 电力系统自动化, 2024, 48(19): 89-100. LIU Yuxin, PENG Ke, ZHAO Zida, et al. Mechanism analysis of power low-frequency oscillations in parallel system of multiple virtual synchronous generators[J]. Automation of Electric Power Systems, 2024, 48(19): 89-100.

　　[19] 苟少云, 郭春义. 构网型与跟网型混合直驱风电场并网稳定域研究[J/OL]. 电力系统自动化[2024-09-29]. http://kns.cnki.net/kcms/detail/32.1180.TP.20240927.1515.010.html. GOU Shaoyun, GUO Chunyi. Grid-connection stability domain study on wind farms with hybrid direct-drive grid-forming and grid-following wind turbines[J]. Automation of Electric Power Systems[2024-09-29]. http://kns.cnki.net/kcms/detail/32.1180.TP.20240927.1515.010.html.

　　[20] 刘欣, 郭志博, 贾焦心, 等. 基于单输入单输出等效序阻抗的微网VSG并网稳定性分析及虚拟阻抗设计[J/OL]. 电工技术学报[2024-05-10]. https://kns.cnki.net/kcms/detail/11.2188.TM.20230419.1615.003.html. LIU Xin, GUO Zhibo, JIA Jiaoxin, et al. Microgrid VSG grid-connection stability analysis and virtual impedance design based on single-input single-output equivalent sequence impedance[J/OL]. Transactions of China Electrotechnical Society[2024-05-10]. https://kns.cnki.net/kcms/detail/11.2188.TM.20230419.1615.003.html.

　　[21] CHOOPANI M, HOSSEINIAN S H, VAHIDI B. New transient stability and LVRT improvement of multi-VSG grids using the frequency of the center of inertia[J]. IEEE Transactions on Power Systems, 2020, 35(1): 527-538.

　　[22] SHEN C, SHUAI Z K, SHEN Y, et al. Transient stability and current injection design of paralleled current-controlled VSCs and virtual synchronous generators[J]. IEEE Transactions on Smart Grid, 2021, 12(2): 1118-1134.

　　[23] 耿华, 何长军, 刘浴霜, 等. 新能源电力系统的暂态同步稳定研究综述[J]. 高电压技术, 2022, 48(9): 3367-3383. GENG Hua, HE Changjun, LIU Yushuang, et al. Overview on transient synchronization stability of renewable-rich power systems[J]. High Voltage Engineering, 2022, 48(9): 3367-3383.

　　[24] 杨银国, 袁枭添, 陆秋瑜, 等. 考虑切换动态的功率同步控制单台构网型换流器暂态稳定性分析[J]. 电网技术, 2023, 47(10): 4005-4016. YANG Yinguo, YUAN Xiaotian, LU Qiuyu, et al. Transient stability analysis of grid-forming converter with power synchronization control considering switching dynamics[J]. Power System Technology, 2023, 47(10): 4005-4016.

　　[25] 唐英杰, 查晓明, 田震, 等. 弱电网条件下虚拟同步机与SVG并联系统的暂态稳定性分析[J]. 电网技术, 2022, 46(10): 4020-4034. TANG Yingjie, ZHA Xiaoming, TIAN Zhen, et al. Transient stability analysis of virtual synchronous generator and SVG parallel system under weak grid conditions[J]. Power System Technology, 2022, 46(10): 4020-4034.

　　[26] ZHANG L D, HARNEFORS L, NEE H P. Power-synchronization control of grid-connected voltage-source converters[J]. IEEE Transactions on Power Systems, 2010, 25(2): 809-820.

　　[27] 姜鑫, 易皓, 卓放, 等. 基于直流电压同步的构网型变流器低频振荡分析与阻尼控制[J]. 电力系统自动化, 2024, 48(16): 30-39. JIANG Xin, YI Hao, ZHUO Fang, et al. Low-frequency oscillation analysis and damping control for grid-forming converters based on DC voltage synchronization[J]. Automation of Electric Power Systems, 2024, 48(16): 30-39.

　　[28] WU H, WANG X F. Design-oriented transient stability analysis of PLL-synchronized voltage-source converters[J]. IEEE Transactions on Power Electronics, 2020, 35(4): 3573-3589.

　　[29] 张宇, 张琛, 蔡旭, 等. 并网变换器的暂态同步稳定性分析: 稳定域估计与镇定控制[J]. 中国电机工程学报, 2022, 42(21): 7871-7884. ZHANG Yu, ZHANG Chen, CAI Xu, et al. Transient grid-synchronization stability analysis of grid-tied voltage source converters: stability region estimation and stabilization control[J]. Proceedings of the CSEE, 2022, 42(21): 7871-7884.

　　[30] PAQUETTE A D, DIVAN D M. Virtual impedance current limiting for inverters in microgrids with synchronous generators[C]// 2013 IEEE Energy Conversion Congress and Exposition, September 15-19, 2013, Denver, USA: 1039-1046.

　　[31] 史蒂芬·H·斯托加茨. 非线性动力学与混沌[M]. 北京: 机械工业出版社, 2018. STROGATZ S H. Nonlinear dynamics and chaos[M]. Beijing: China Machine Press, 2018.