半封闭式薄壁结构的耐撞性研究及优化

　　薄壁结构凭借轻量化、易于生产、吸能性好等优异特点，广泛应用于汽车、航空航天等领域。在传统吸能结构基础上，本文提出一种半封闭式薄壁结构，对比了4种截面形状(三角形、方形、六边形、八边形)下半封闭铝合金薄壁管与普通裸管的耐撞性。模拟结果显示，半封闭式薄壁管的吸能性能优于普通裸管，其中半封闭方形管结构的能量吸收能力最强，比吸能高达17952.20 J·kg⁻¹，相较于方形裸管提高了110%。研究发现，螺距为20 mm、圈数为2的半封闭式薄壁管耐撞性能较好。最后，利用响应面法对半封闭管件结构进行优化，结果表明：优化后薄壁结构的厚度为2.496 mm、肋板厚度为0.826 mm、螺距为21.800 mm，比吸能较优化前提高了58.04%。研究结果为半封闭结构的实际应用提供了一定的理论依据。

　　关键词：薄壁结构;半封闭;响应面法;耐撞性;吸能性能

　　论文《半封闭式薄壁结构的耐撞性研究及优化》发表在《锻压技术》，版权归《锻压技术》所有。本文来自网络平台，仅供参考。

　　引言

　　能量吸收能够减少关键部件的损坏，减轻事故中不必要的影响，而薄壁结构可通过牺牲塑性变形吸收关键部件承受的冲击动能，在汽车、航空航天等领域应用广泛。薄壁结构的能量吸收能力受截面边数、胞数、材料等多种设计因素影响，传统研究多聚焦于全封闭式或全开口薄壁结构。

　　全封闭式薄壁结构能量吸收稳定，但吸能效率有限;全开口薄壁结构虽比吸能更高，却存在失稳变形模式不稳定、难以实现可控渐进变形的问题。现有研究中，针对半封闭式薄壁结构的探索较少。本文旨在结合封闭与开口结构的优势，设计一种半封闭式薄壁结构，研究其吸能性能，筛选能量吸收最优的结构形式，并通过优化几何参数进一步提升吸能性能、稳定变形模式。

　　1 半封闭式薄壁结构设计及有限元模型建立

　　1.1 几何结构设计

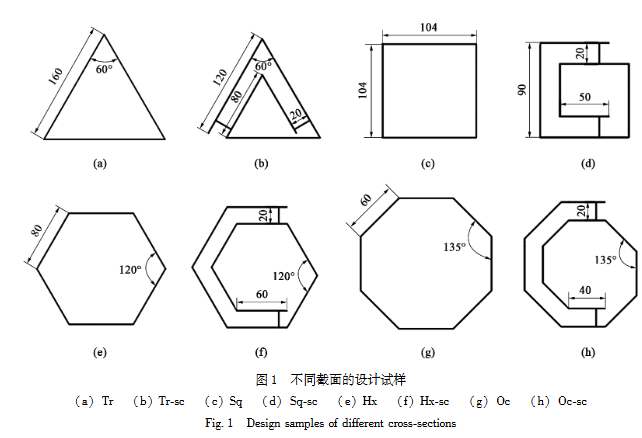
　　本文设计了4种对称截面结构(三角形、方形、六边形、八边形)，分别对对应的薄壁裸管和半封闭管进行轴向压缩对比。截面编码规则为：三角形(Tr)、方形(Sq)、六边形(Hx)、八边形(Oc)，半封闭结构标注为“sc”，即Tr-sc、Sq-sc、Hx-sc、Oc-sc。

　　所有半封闭式结构的高度均为300 mm，初始螺距为20 mm，圈数为2。材料选用6061-T6铝合金，兼顾强度与轻量化需求，其减轻率达55.4%，且模态和刚度优于钢制材料。

　　1.2 耐撞性指标

　　选取4项核心指标评价半封闭薄壁结构的耐撞性能：

　　1. 初始峰值载荷(Fₘ)：压溃变形初始阶段的最大峰值力，过大易产生危险加速度;

　　2. 总能量吸收(EA)：由力-位移曲线积分得到，反映结构整体吸能能力;

　　3. 比吸能(SEA)：单位质量的能量吸收效率，计算公式为SEA=EA/m(m为薄壁结构总质量);

　　4. 碰撞力效率(CFE)：衡量结构载荷均匀度，计算公式为CFE(d)=MCF(d)/Fₘ×100%=EA(d)/(d×Fₘ)×100%(MCF为平均冲击力)。

　　1.3 有限元建模

　　采用ABAQUS/Explicit对不同截面薄壁管的吸能性能进行对比分析。模型包含上下刚性板和薄壁铝合金结构，上刚性板沿Z轴下压200 mm(准静态轴向压缩)，下刚性板固定不动。

　　6061-T6铝合金的材料参数为：密度2.8×10⁻⁶ kg·mm⁻³，弹性模量68200 MPa，泊松比0.33。薄壁管与上下刚性板采用面面接触，薄壁管采用自接触，罚函数系数为0.2，单元网格大小为2 mm×2 mm×2 mm。

　　2 结果分析与讨论

　　2.1 力-位移曲线特征

　　不同截面形状裸管和半封闭管的力-位移曲线变化趋势基本一致，但半封闭式薄壁管的载荷波动更小，结构稳定性更优。由于半封闭式薄壁管质量更大，其初始峰值力和整体载荷高于普通裸管。

　　当金属薄壁管受到准静态轴向冲击载荷时，载荷随位移线性增加，下压至1 mm左右达到初始峰值载荷(初始弹性屈曲阶段);随后刚性板继续压缩，薄壁管出现褶皱，进入相对稳定的渐进屈曲阶段，此阶段为能量吸收的主要阶段。

　　2.2 变形模式分析

　　轴向压缩下，薄壁结构呈现渐进折叠模式，随着边数增加，薄壁管产生的褶皱更多。普通裸管以稳定的对称手风琴变形模式为主，半封闭式薄壁管先以对称手风琴模式变形，后切换至整体屈曲变形。

　　半封闭似螺旋结构的管壁间存在空隙，增大了变形空间，且空隙间增设的两条肋板与管壁相互作用，进一步提升了能量吸收效果。

　　2.3 吸能指标对比

　　数值模拟结果显示，普通薄壁结构的总吸能随边数增加而提高(八边形>六边形>方形>三角形)。与普通裸管相比，4种半封闭式薄壁结构的耐撞性均显著提升：

　　- SEA分别提高122.45%(Tr-sc)、80.16%(Sq-sc)、62.51%(Hx-sc)、45.65%(Oc-sc);

　　- CFE分别提高14.45%(Tr-sc)、9.60%(Sq-sc)、6.74%(Hx-sc)、30.59%(Oc-sc)。

　　综合分析可知，半封闭方形管(Sq-sc)表现出最优异的性能，其比吸能高达17952.20 J·kg⁻¹，相较于方形裸管提高110%。

　　3 半封闭式薄壁结构几何参数优化

　　3.1 几何参数设计

　　以半封闭方形管(Sq-sc)为优化基础，研究螺距、对称结构、圈数对耐撞性的影响：

　　- 螺距(P)：选取20 mm、30 mm、40 mm三个水平;

　　- 结构形式：在螺距20 mm基础上设计2种非对称结构(Sq-sc-a、Sq-sc-b)，并与对称结构对比;

　　- 圈数：选取2、3、4三个水平。

　　3.2 几何参数结果对比

　　数值模拟结果表明：

　　1. 螺距影响：随着螺距增加，比吸能单调减小，每增加10 mm，比吸能平均减少11.99%，碰撞力效率基本保持一致;

　　2. 圈数影响：随着圈数增加，比吸能单调减小，每增加1圈，比吸能平均减少15.02%;

　　3. 结构对称性影响：非对称结构的比吸能平均减少8.07%，CFE均变小，说明对称结构受力更均匀、稳定性更好。

　　综上，螺距为20 mm、圈数为2的对称方管耐撞性能最优。

　　4 半封闭式吸能构件尺寸优化

　　4.1 优化模型建立

　　采用响应面法(RS)进行多目标优化，以比吸能(SEA)最大化为核心目标，初始峰值载荷(Fₘ)最小化为次要目标。设计变量为壁厚(T₁)、肋厚(T₂)和螺距(P)，约束条件为：

　　- 0.5 mm ≤ T₁ ≤ 2.5 mm;

　　- 0.5 mm ≤ T₂ ≤ 2.5 mm;

　　- 10 mm ≤ P ≤ 20 mm。

　　由于SEA和Fₘ数值量级不同，先进行归一化处理，再引入权重系数(u=0.7，v=0.3)将多目标问题转化为单目标优化，最终优化函数为：Max[y(*)=u y₁ - v y₂](y₁为归一化SEA，y₂为归一化Fₘ)。

　　4.2 优化结果验证

　　响应面模型拟合精度较高(SEA的R²值接近1.000，Fₘ的R²=0.964)，最优参数组合为：

　　- 壁厚(T₁)：2.496 mm;

　　- 肋板厚度(T₂)：0.826 mm;

　　- 螺距(P)：21.800 mm。

　　优化后模型的吸能性能较原Sq-sc结构显著提升：

　　- 总能量吸收(EA)：从7838.67 kJ提升至20681.02 kJ，增幅163.83%;

　　- 比吸能(SEA)：从17952.20 J·kg⁻¹提升至28371.48 J·kg⁻¹，增幅58.04%;

　　- 初始峰值载荷(Fₘ)：从73.54 kN提升至137.28 kN，增幅86.67%;

　　- 碰撞力效率(CFE)：从0.5330提升至0.7532，增幅41.31%。

　　优化后模型的载荷波动更小，耐撞性和稳定性均得到有效提升。需注意的是，实际应用中需控制吸能管件厚度，避免因厚度过大导致初始峰值载荷过高引发危险。

　　5 结论

　　1. 与传统普通裸管相比，4种半封闭式薄壁管的耐撞性均显著提升，其中半封闭方形管(Sq-sc)的比吸能最高(17952.2 J·kg⁻¹)，相较于方形裸管提高110%。

　　2. 螺距和圈数对半封闭式薄壁结构的耐撞性有显著影响：初始峰值载荷和总吸能随螺距、圈数增加而增大(因结构质量增加)，但比吸能随二者增加而减小(单位质量吸能能力下降)。

　　3. 对称结构的耐撞性优于非对称结构，对称结构受力稳定、载荷波动小;螺距20 mm、圈数2的半封闭方形管具有优异的耐撞性能。

　　4. 基于响应面优化方法，当壁厚2.496 mm、肋厚0.826 mm、螺距21.800 mm时，半封闭式薄壁管的比吸能达到28371.48 J·kg⁻¹，耐撞性显著提升，可为实际工程应用提供理论支撑。

　　参考文献

　　[1] Alexander M J. An approximate analysis of the collapse of thin cylindrical shells under axial compression[J]. International Journal of Mechanical Sciences, 1960, 13(1):10-15.

　　[2] Mamalis G, Johnson W. The quasi-static crumpling of thin frusta and cylinders[J]. International Journal of Mechanical Sciences, 1983, 25(9-10):713-732.

　　[3] Mamalis G, Manolakos D E, Baldoukas A. Comparative analysis of energy absorption of thin-walled tubes with triangular, polygonal and octagonal sections[J]. Thin-Walled Structures, 1991, 12(1):17-34.

　　[4] Nia A, Parsapour A, Parsapour M. Comparative analysis of energy absorption and failure modes when axially loading multi-cell thin-walled tubes[J]. Thin-Walled Structures, 2014, 74:155-165.

　　[5] Wu S Z, Huang X, Wang J Q, et al. On design of multi-cell thin-walled structures for crashworthiness[J]. Thin-Walled Structures, 2018, 127:169-179.

　　[6] 林启权, 刘雯婷, 王凯, 等. 多胞薄壁结构优化及结构参数对耐撞性影响分析[J]. 振动与冲击, 2024, 43(16):60-66+110.

　　[7] Cetin E, Baykasoğlu C. Energy absorption of thin-walled tubes enhanced by lattice structures[J]. Thin-Walled Structures, 2023, 279:115626.

　　[8] Ma J Y, Chai S Y, Chen B. Geometric design, deformation mode, and energy absorption of patterned thin-walled structures[J]. International Journal of Mechanical Sciences, 2019, 157-158:471-484.

　　[9] Wang K, Sun G Y, et al. Reversible energy absorption of shape-memory thin-walled structures[J]. Materials & Design, 2022, 168:104269.

　　[10] 张海燕, 周国华. 汽车防撞栏仿竹薄壁管结构的能量吸收特性[J]. 机械强度, 2024, 46(4):831-838.

　　[11] 陈雅婷, 洪熠豪, 吴俊, 等. 仿生多胞薄壁结构冲击吸能特性研究[J]. 机械强度, 2024, 46(3):750-755.

　　[12] Ren Y R, Xiang J W. Influences of geometrical factors on the crashworthiness of open shells[C]. Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, 2010.

　　[13] Hirokazu Shoji, Takahira Aoki. Improvements on impact energy absorbing ability of open section short columns[C]. Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Orlando, 2010.

　　[14] 毕思蕊. 开口薄壁结构的能量吸收与耐撞性研究[D]. 大连:大连理工大学, 2015.

　　[15] Liu S, Wang J Q, Huang X, et al. Bending responses of aluminum mortise-tenon joints in lightweight electric vehicle inspired by timber structures[J]. Thin-Walled Structures, 2024, 43(16):60-66+110.

　　[16] 张西富, 马鸣图, 王刚刚, 等. 6061T6铝合金前防撞梁的开发与应用[J]. 铝加工, 2018(5):15-20+37.

　　[17] 马箫, 苗诗梦. 肋板对吸能构件耐撞性的影响及优化设计[J]. 锻压技术, 2023, 48(5):314-320.

　　[18] Hou S, Han G, Sun G Y, et al. Multiobjective optimization of multi-cell thin-walled tubes for crashworthiness[J]. Thin-Walled Structures, 2011, 49(7):855-863.

　　[19] Yin F, Wen G L, Hou S J, et al. Crushing analysis and crashworthiness optimization of honeycomb-filled single and polygonal tubular structures[J]. Materials & Design, 2011, 32(8-9):4449-4460.