机械密封热变形仿真及其对润滑性能的影响研究

　　为了解决机械密封在高温、高压、高速等极端工况下的安全性问题，针对工作在高温环境下的涡轮泵螺旋槽机械密封变形的量化及其影响问题，开展了热变形方面的研究。首先，分析了涡轮泵机械密封的结构和使用工况;然后，建立了润滑性能分析模型，并计算了机械密封在工作时动环和静环之间的液膜力;最后，使用有限元仿真的方法获得了机械密封在高温和液膜力作用下的变形量，分析了变形对机械密封润滑性能的影响，并将理论数据与试验数据进行了对比。研究结果表明：液膜力为2 kN时，得到了机械密封动环和静环的变形量，动环最大变形量为8.3 μm，静环最大变形量为0.6 μm;考虑变形后，机械密封的最小润滑膜厚(h_{min})较不考虑变形时的膜厚h要小，而流量Q较不考虑变形时要大;理论计算结果和试验结果更加接近，证明了理论分析的正确性。该研究结果可为高参数机械密封的相关设计及性能仿真研究提供参考。

　　关键词：涡轮泵;非接触式机械密封;螺旋槽机械密封;SolidWorks实体建模;液膜力计算;开启力;泄漏量

　　论文《机械密封热变形仿真及其对润滑性能的影响研究》发表在《机电工程》，版权归《机电工程》所有。本文来自网络平台，仅供参考。

　　0 引言

　　机械密封是一种用于控制和防止流体泄漏的密封装置，其特点是可靠性强、使用寿命长，被广泛应用于石油、化工、能源、航空航天、核工业等领域[1-3]。机械密封可防止流体从设备内部泄漏或进入设备内部，起到保护设备和环境的作用[4-6]。

　　由于经常被应用于一些高温、高压等极端场合，机械密封在使用时的可靠性也越来越受到业界的广泛重视[7-8]。与接触式密封相比，非接触式密封结构能够在端面之间形成润滑，从而提高其密封的实际性能[9-12]。

　　目前已有许多学者对机械密封变形等相关问题进行了研究。赵天琦等人[13]建立了超高速齿轮箱机械密封热流-固耦合仿真模型，进行了超高速传动系统径向双端面机械密封端面的温升及变形研究，其结论可为涡轮泵机械密封的仿真计算提供参考。谢玉汉等人[14]针对机械密封的端面变形问题，进行了膜压、膜厚、温度和变形之间的耦合求解，研究了转速、密封压力和介质温度对上游泵送机械密封端面变形的影响规律;但其结论缺少极端工况参数下的验证。顾广溪等人[15]采用有限差分法，求解了密封的压力分布、开启力和泄漏量，分析了端面波度几何参数及密封工况参数对机械密封开启力、泄漏率的影响规律;但其未将温度的影响考虑在内，因此其结论存在一定的局限性。宋玉鹏[16]通过计算获得了密封端面的温度、应力、变形等变化规律，同时通过试验证明了上述模型的准确性，该研究工作较为完整，对机械密封相关研究具有很好的参考价值。殷润生等人[17]研究了机械密封的摩擦副密封环在干摩擦运转时单力场及热力变形下的磨损深度，并用磨损理论值对结论进行了验证，其结果可作为机械密封磨损研究方面的参考。刘帅[18]采用有限元分析法和实验法，研究了密封环组件的变形规律、应力分布和温度分布，探讨了导致密封环变形的主要因素;该结果对机械密封的有限元仿真研究具有较好的参考价值。李勇凡等人[19]采用实验测试的方式，分析了机械密封端面磨损的形成机理，得到了两种弹簧力条件下温升和位移的演变数据，其结论可为机械密封的减磨设计提供参考。张文豪[20]进行了机械密封端面变形影响因素分析与调控方法研究，得到了不同结构密封端面的温度、应力等分布情况，其结论可对相关密封试验结果提供理论依据。张鹏高等人[21]基于窄槽理论，计算了磁流体润滑螺旋槽机械密封的压力场和磁流体膜开启力，分析了结构参数对磁流体膜厚度、密封环角变形的影响，其可为螺旋槽机械密封相关研究提供参考。GLIENICKE J等人[22]进行了高压、高速下机械密封的数值模拟和实验研究，其结果表明，高压、高速情况下，在密封端面形成稳定的全膜润滑以避免局部干摩擦现象的方法是可行的，该研究可以为密封端面的减摩设计提供参考。LEBECK A O[23]在考虑了机械密封端面波度、锥度和粗糙度的基础上，建立了机械密封的泄漏模型，研究结果证明，该密封泄漏模型对机械密封实际工况下的性能研究具有较好参考价值。

　　从以上分析可见，对机械密封热问题的分析很重要，并且已经有很多的仿真及试验研究结果可供参考。针对螺旋槽机械密封变形的量化及其影响问题，笔者从设计的角度出发，针对机械密封的实际使用工况，使用流体润滑计算和有限元仿真相结合的方法，讨论机械密封的变形问题、动环设计尺寸的优化问题，以及变形对润滑膜厚度、泄漏量的影响。

　　1 机械密封的使用背景及工况分析

　　相对于其他轴封装置，机械密封的应用较为普遍，其原因在于机械密封的制造比较简单，并且具有结构相对简单、维护成本低且稳定性、密封性好等优点。

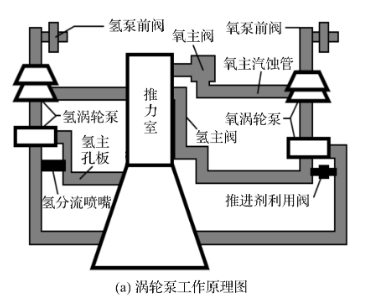
　　本研究的对象为螺旋槽机械密封，其主要应用对象是火箭发动机涡轮泵，而涡轮泵是液体火箭发动机的心脏。图1(a)为火箭发动机涡轮泵工作原理图，涡轮泵主要功能是把推进剂输送到主推力室中生成燃气，并高速从喷管中喷出从而产生推力。图1(b)为涡轮泵机械密封的结构图，机械密封主要由动环、静环、波纹管等组成。

　　非接触式机械密封端面之间的摩擦磨损极小，甚至不存在摩擦磨损，因此其使用寿命较长、密封性能可靠。此种密封在动环和静环之间形成一层微米级的流体薄膜，这层薄膜将两端面分开，使得密封的动环和静环在旋转时保持非接触状态。这层流体动压液膜的存在使得机械密封端面避免了干磨损，降低了机械密封的摩擦磨损，提高了密封系统的抗干扰能力和使用寿命。

　　涡轮泵机械密封工况参数如表1所示。

　　表1 涡轮泵机械密封工况参数

　　| 参数/单位 | 数值 |

　　| 转子转速n/(r/min) | 0~30000 |

　　| 工作温度T/℃ | 600~700 |

　　| 介质黏度μ/(Pa·S) | 0.6×10⁻³~1.5×10⁻³ |

　　| 压差ΔP/MPa | 0.5~5.0 |

　　| 轴向载荷W/kN | 5~10 |

　　| 介质温度T₁/℃ | -252~-160 |

　　2 机械密封动、静环变形仿真

　　在进行机械密封动环和静环热变形分析时，使用ANSYS Workbench软件作为工具。热变形的有限元仿真流程如图2所示。根据图2，首先根据流体润滑理论以及机械密封的结构、使用工况，通过计算获得机械密封在给定工作转速n、工作间隙h下的液膜力F，再将计算结果带入有限元模型中获得液膜温度T，最后通过有限元仿真获得机械密封热变形δ的大小和分布规律。

　　2.1 机械密封的数字化建模

　　涡轮泵机械密封动环的二维结构图如图3所示。机械密封主要参数包括内外径及螺旋槽相关参数等，其中，与动环相关的结构尺寸参数如表2所示。

　　表2 机械密封的尺寸参数

　　| 参数/单位 | 数值 |

　　| 动环外径D₁/mm | 145 |

　　| 动环内径d₁/mm | 106 |

　　| 动环厚度H₁/mm | 8 |

　　| 静环外径D₂/mm | 145 |

　　| 静环内径d₂/mm | 117 |

　　| 静环厚度H₂/mm | 10 |

　　| 槽底圆直径d/mm | 115 |

　　| 螺旋槽数量N₉ | 12 |

　　| 螺旋槽深h₉/μm | 5 |

　　| 螺旋角α/(°) | 15 |

　　| 螺旋槽宽比B | 0.5 |

　　螺旋槽的槽台边界曲线为对数螺旋线，其参数方程如下式所示(r为对数螺旋线半径，α为对数螺旋线的螺旋角，即螺旋线的切线与动环圆柱面母线所夹的锐角;θ为沿坐标轴的极位夹角)。

　　在使用SolidWorks软件进行实体建模的过程中，将机械密封动环和静环的主体结构视为圆柱，再通过拉伸基体操作建立其模型;在绘制螺旋槽时，选择将密封动环上表面作为基准面，并选择圆周阵列，将螺旋线旋转15°，以获得单周期的螺旋槽，选择“拉伸切除”命令，切除深度为5 μm，最后生成螺旋槽。

　　涡轮泵机械密封固体域动、静环模型如图4所示(仿真计算之前已对动、静环模型结构进行了简化，以方便后续的仿真计算)。动环模型选择圆周阵列，以Y轴为旋转中心阵列目标;静环通常镶嵌在静环座上，材料采用强度较高的环氧树脂浸渍石墨，建模时进行了简化。

　　2.2 机械密封的液膜力计算

　　非接触式机械密封的液膜厚度h、液膜力F和泄漏量Q等是反映其性能的主要因素，因此在进行机械密封热变形分析之前，首先需获知液膜力F的大小。

　　非接触式机械密封的理论分析模型如图5所示。当主轴不工作时，静环受到弹性元件的压紧力作用，其与动环紧密贴合在一起，起到阻止密封介质泄漏的作用;当主轴开始转动，密封介质通过动环端面动压槽的泵送效应被输送到密封端面处，增强了动环和静环表面的动压效应，强化了机械密封的开启性，并使动、静环端面分离脱开。

　　用于分析的广义雷诺方程极坐标形式如下式所示(h为机械密封的动环和静环之间的密封间隙;ρ为动环和静环之间润滑介质的密度;μ为润滑介质的动力黏度;n为动环的转速;V为动环与静环之间的挤压速度;p为动环和静环之间形成液膜的压力)。

　　取一参考平面与静环表面相重合，当动、静环平面距离为(h₀)时，动环和静环间的密封间隙可由下式获得(φ为动环轴线与z轴的夹角在y-z平面上的投影角;γ为动环轴线与z轴在x-z平面上的投影角;(h₉)为螺旋槽的深度;θ的起始线与y轴重合，当动环上开有深度(h_c)的螺旋槽时，在非槽区中(h₉=0)，在槽区中(h₉=h_c))。

　　对液膜压力P求端面面积上的积分得到润滑膜力F，如下式所示：(F = ∬_Ω P dΩ)。

　　螺旋槽机械密封液膜力的计算流程如图6所示。根据前期研究中获得的机械密封快速启停的试验数据，结合理论进行计算，获得了机械密封液膜力F。

　　机械密封快速启停试验的时间t为250s，试验时测得了涡轮泵转子的转速n和机械密封的液膜厚度h。n和h随t的变化关系以及机械密封液膜力F随t的变化关系如图7所示。

　　从图7(a)中可以看出：在试验开始的阶段，短时间内转速n迅速升至3×10⁴ r/min的额定转速，150s后转速逐渐降低直至为0。从图7(b)中可以看出，液膜厚度h的大小跟转速n密切相关，当试验时间t在50~150s之间时，h的大小为6 μm左右，而后h随n的降低逐渐减小至0。从图7(c)中可以看出，机械密封在工作时F的变化范围在0 kN~2.1 kN之间。在运行的开始和结束阶段，因为转速较低，所以动压产生的液膜力很小;在中间运行阶段，转速达到了几万转，此时机械密封静环和动环之间的液膜力达到了最大值。

　　2.3 螺旋槽机械密封的变形分析

　　机械密封动环和静环的相关材料参数如表3所示。

　　表3 机械密封的相关材料参数

　　| 参数/单位 | 动环数值 | 静环数值 |

　　| 弹性模量E/GPa | 213 | 120 |

　　| 泊松比μ | 0.254 | 0.27 |

　　| 线膨胀系数γ/K⁻¹ | 11.8×10⁻⁶ | 4.8×10⁻⁶ |

　　| 导热系数λ/(W·m⁻¹·K⁻¹) | 20 | 10.8 |

　　| 比热容Cₚ/(J·kg⁻¹·K⁻¹) | 434.6 | 748 |

　　实体模型导入后，需要指定分析对象的特征，即定义单元类型，用来模拟工程中的各种结构和材料。结构分析中应该考虑的参数有弹性模量、泊松比，热分析应该考虑导热系数等。

　　从“稳态热”模块中打开已导入的模型，选择“工程数据”，对动环模型的材料和相关材料系数进行定义(研究对象的动环材料为9Cr18，静环采用浸渍石墨);在进行有限元分析时，先将机械密封动环表面的螺旋槽进行简化。

　　模型导入后，划分好网格的动环模型、静环模型如图8所示。对于划分网格部分，选择Mesh模块，定义实体网格尺寸为0.5 mm。由于不存在比例过大的问题，因此，对于动环的网格划分采用常用的六面体网格或者混合网格皆可。

　　为了方便密封环的温度场仿真计算，进行如下假设：

　　1) 密封环端面间为理想水平间隙，热量均匀地分布在模型表面;

　　2) 密封环材料物性参数为恒定值，不随边界条件的变化而变化;

　　3) 密封介质和外部空气的流体对流换热系数不随流体的温度变化而改变;

　　4) 忽略密封环端面间的碰磨和摩擦磨损热，密封端面间为完全流体润滑;

　　5) 密封端面与润滑液膜充分接触，不存在空隙，并且液膜与壁面间充分换热;

　　6) 不考虑热辐射影响和重力因素的影响。

　　完成网格划分后，开始进行热变形量的分析。根据密封环的工作状况，可得到动环和静环的边界条件设置情况、动环端面施加载荷后的模型图，如图9所示。

　　因为动、静环端面与液膜接触，承受端面液膜动压力，所以在计算时，将动环和静环端面设置为流固耦合面;静环后端外侧和内侧通过静环座进行固定，采用环形约束的形式进行固定，并在其背侧添加轴向位移约束;动环外侧和背侧加载压力与密封介质压力相同，内侧设置为标准大气压，动环内侧因为需要与转子进行固定，所以计算中对动环内侧采用环形约束，并在其背侧进行固定约束。

　　动环和静环的工作端面施加均布载荷为2 kN，温度边界条件按照静环和动环内侧-160 ℃、外侧500 ℃、工作端面-160 ℃、背面500 ℃进行施加。

　　由图9可知：给动环模型施加温度和载荷后，温度和载荷最大的区域为螺旋槽所在区域;动环的内侧和外侧相比其他区域，受到的温度和载荷都较低。

　　动环和静环的热变形有限元分析结果如图10所示。图10(a)为考虑压力和温度时动环的仿真结果，从中可以看出：动环产生较大变形的地方是在外侧，最大变形量为8.3 μm，此时最大变形量已和机械密封工作时的液膜厚度相当，这对涡轮泵机械密封性能会产生重要影响。

　　图10(b)为静环的仿真结果，从中可以看出：因涡轮泵机械密封静环为浸渍石墨材料，线膨胀系数为4.8×10⁻⁶ K⁻¹，远远小于金属热膨胀系数，所以受热后的变形量很小;并且石墨材料的塑性不强，受力后的变形量也很小，因此，静环仿真得到的变形量非常小，且为静环的固体边界约束点偏内侧方向，所以静环的最大变形量在其外侧，最大变形量为0.6 μm。

　　由以上的变形结果分析可知，静环在端面压力和温差的作用下产生的变形极小。机械密封的润滑膜厚一般在微米量级，其轴向的变形量远小于工作膜厚，因此，变形对密封流场的影响可忽略不计。

　　3 机械密封热变形对其润滑性能影响

　　由前面的有限元仿真结果可知：机械密封在工作时，动环比静环产生的变形要大得多，动环的变形量沿着外径的方向越来越大，最大变形量可达8.3 μm。动环的外侧产生了较大变形，最大变形区为大温差下外侧轴向变形，内侧变形量较小，使整个密封端面呈现为锥形的结构。

　　在变形后，机械密封的动环表面和静环表面将不再平行，因此前面介绍的机械密封润滑性能计算模型中的膜厚公式需要进行修正，此时机械密封的液膜厚度可用两个量表达，即最小膜厚(h_{min})和最大膜厚(h_{max})。根据动环的变形特点可知，(h_{min})在机械密封的最里端，(h_{max})在机械密封的最外端。

　　机械密封液膜厚度如图11所示。因机械密封变形前后的载荷不变，所以对液膜进行积分所得的液膜力是相等的，未考虑变形的膜厚h介于(h_{max})和(h_{min})之间。

　　假设机械密封沿着半径方向的变形增量是相同的，那么就有变形后任意一点的膜厚(h')如下式所示(R为密封动环外半径，r为动环上任意一点位置处的半径)。图11中的( heta₁)可根据有限元仿真结果和机械密封动环的变形量计算获得。

　　在进行润滑性能的计算分析时，将变形后的最小膜厚(h_{min})与变形前的膜厚h进行对比，同时对比变形前后泄漏量的变化。

　　膜厚和泄漏量随转速变化的计算结果如图12所示。图12(a)为膜厚随转速变化的计算结果，从中可以看出，变形前后的润滑膜厚均随着转速n的增加而增大;在n相同时，h介于(h_{max})和(h_{min})之间;如果在计算时未考虑变形影响，获得的膜厚计算结果会比实际最小膜厚值大1.5 μm左右，这样的设计会使机械密封在低转速时发生磨损。

　　图12(b)为泄漏量Q随转速n变化的计算结果，从中可以看出，在考虑变形后的Q比不考虑变形时的值要大，原因在于变形后动环和静环之间的间隙增大，使得Q也增大。

　　接下来，在机械密封试验系统中进行密封的性能测试。其中，机械密封试验系统实物如图13所示。该试验测试系统主要由驱动系统、试验腔体、加载装置和密封介质等几部分组成。试验条件及机械密封试验件的结构和尺寸与前面理论计算时相同。

　　机械密封膜厚和泄漏量的试验测试数据，如图14所示。从图14(a)中可以看出，随着转速的增加，h从5000 r/min时的2 μm，逐渐增大到了30000 r/min时的8 μm;试验获得的膜厚数据介于图12(a)中的变形后最小膜厚(h_{min})和最大膜厚(h_{max})之间，符合实际情况。

　　从图14(b)中泄漏量Q的试验测试数据可以看出：随n的增大，Q的值也在逐渐增大，从5000 r/min时的0.7 mL/s，逐渐增大到了30000 r/min时的3.3 mL/s。

　　与图12(b)中的泄漏量理论计算数据相比，试验获得的泄漏量值与考虑变形的泄漏量计算结果更为接近，这也证明了理论分析的正确性[26]。

　　4 结束语

　　为了解决机械密封在高温、高压、高速等极端工况下的安全性问题，针对工作在高温环境下的涡轮泵螺旋槽机械密封变形的量化及其影响问题，开展了热变形方面的研究。

　　使用流体润滑计算和有限元仿真相结合的方法，讨论了机械密封的变形问题、动环设计尺寸的优化问题，以及变形对润滑膜厚度、泄漏量的影响。

　　研究结论如下：

　　1) 静环在端面压力和温差的作用下产生的最大变形量在静环的外侧，变形极小，仅0.6 μm。其轴向的变形量远小于工作膜厚，因此，其变形对密封流场的影响可忽略不计;

　　2) 动环产生较大变形的地方是在外侧，最大变形量为8.3 μm，最大变形量已和机械密封工作时的液膜厚度相当，这对涡轮泵机械密封性能产生了重要影响;

　　3) 在转速相同时，不考虑机械密封变形获得的膜厚h在考虑变形时获得的最大膜厚和最小膜厚之间;如果在计算时未考虑变形影响，那么膜厚计算结果会比实际最小膜厚大1.5 μm左右，这样的设计会使机械密封在低转速时发生磨损;

　　4) 对于机械密封，在试验台上进行了性能测试，从试验结果可知，测得的膜厚数据h在考虑变形时计算获得的最大膜厚和最小膜厚之间，泄漏量Q的试验测试数据与考虑变形的泄漏量计算结果更为接近，证明了理论分析的正确性。

　　上述理论和试验研究结果可为高参数机械密封的设计和试验提供参考。

　　后续，将继续探索机械密封在高温下变形量的实测技术，以期对机械密封静环和动环的变形量进行理论和试验对比。

　　参考文献

　　[1] 王晓虎. 极端工况机械密封的结构设计和摩擦学性能试验研究[D]. 西安: 西安理工大学机械与精密仪器工程学院, 2019.

　　[2] 张琛. 火箭发动机涡轮泵机械密封的磨损机理及性能优化[D]. 西安: 西安理工大学机械与精密仪器工程学院, 2019.

　　[3] 王小丽, 尚雪梅, 刘希, 等. 涡轮泵超导磁力与液膜力复合机械密封性能仿真研究[J]. 润滑与密封, 2023, 48(10):8-13.

　　[4] LIU Yan. 我国成功发射可重复使用试验航天器(英文)[J]. Aerospace China, 2020, 21(3):59.

　　[5] GAO Chun-yang, YU Xiang-yang, NAN Hai-peng, et al. Stability and dynamic analysis of doubly-fed variable speed pump turbine governing system based on Hopf bifurcation theory[J]. Renewable Energy, 2021, 175(9):568-579.

　　[6] 李建克, 刘晨阳, 雷龙生, 等. 基于公理设计理论的高工况螺旋槽机械密封优化方法[J]. 西北工业大学学报, 2023, 41(4):704-711.

　　[7] 张文虎, 李文超, 邓四二, 等. 某液体火箭发动机涡轮泵球轴承故障机理及改进方案[J]. 航空动力学报, 2021, 36(2):396-404.

　　[8] 贾谦, 王建磊, 崔展, 等. 引入螺旋槽制造误差的机械密封性能分析及优化[J]. 西安交通大学学报, 2020, 54(11):46-55.

　　[9] 戴屹梅, 张和生, 方柯. 基于导航定位原理的火箭涡轮泵轴承故障诊断[J]. 宇航学报, 2019, 40(3):286-294.

　　[10] 张国渊, 赵伟刚, 闫秀天, 等. 基于POD降阶模型的非接触端面密封动态监测原理及仿真[J]. 航空学报, 2012, 33(2):354-361.

　　[11] 张树强, 李双喜, 蔡纪宁, 等. 动静压混合式气体密封追随性及主动调控振动特性数值分析[J]. 航空学报, 2012, 33(7):1336-1346.

　　[12] 王建磊, 张琛, 王晓虎, 等. N₂O₄环境下液体火箭发动机涡轮泵机械密封浸渍石墨的磨损机理研究[J]. 机械工程学报, 2019, 55(7):119-127.

　　[13] 赵天琦, 伊进宝, 文孟刚, 等. 超高速传动系统径向双端面机械密封端面温升及变形研究[J]. 机械传动, 2024, 48(10):138-147.

　　[14] 谢玉汉, 孟祥铠, 赵文静, 等. 高压工况上游泵送机械密封热力变形与密封性能分析[J]. 化工学报, 2023, 74(10):4241-4251.

　　[15] 顾广溪, 宋源森, 白少先. 弹性变形对泵用高速波度端面机械密封液体泄漏特性的影响[J]. 润滑与密封, 2023, 48(7):184-189.

　　[16] 宋玉鹏. 釜用剖分式机械密封温升变形特性及试验研究[D]. 北京: 北京化工大学机电工程学院, 2023.

　　[17] 殷润生, 穆塔里夫·阿赫迈德, 耿军. 热力变形下渣浆泵机械密封干摩擦磨损分析[J]. 润滑与密封, 2023, 48(4):61-67.

　　[18] 刘帅. 伺服系统超高速机械密封热力变形研究[J]. 设备管理与维修, 2023, 44(7):45-46.

　　[19] 李勇凡, 宋勇, 郝木明, 等. 涡轮泵用球面装配机械密封热变形及磨损特性实验研究[J]. 中国机械工程, 2023, 34(13):1550-1558.

　　[20] 张文豪. 高参数典型机械密封环端面变形影响因素分析与调控方法研究[D]. 北京: 北京化工大学机电工程学院, 2023.

　　[21] 张鹏高, 顾伯勤, 周剑锋, 等. 磁流体润滑螺旋槽机械密封环角变形计算[J]. 南京工业大学学报:自然科学版, 2022, 44(4):405-411.

　　[22] GLINEICKE J, LAUNERT A, SCHLUNS H, et al. Non-contracting Gas Lubricated Face Seals for High PXV Values[R]. NASA Lewis Research Center, Seals Flow Code Development, 1993:367-379.

　　[23] LEBECK A O. Hydrodynamic lubrication in wavy contacting face seals-a two-dimensional model[J]. Journal of Lubrication Technology, 1981, 103(4):578-586.

　　[24] LIU Lu. Experimental study on end film pressure of mechanical seal under variable operating conditions[J]. Lubrication and Sealing, 2012, 37(2):45-48.

　　[25] SONG Li-qun, LIU Lu, WU Qun, et al. Experimental research on anti-deformation mechanical seal and its application in 100Y Ⅱ-120 pump[J]. Petrochemical Equipment Technology, 1999(3):36-38,4-5.

　　[26] 曾群锋, 梁艳. 核主泵用机械密封摩擦学性能研究进展[J]. 液压气动与密封, 2024, 44(4):15-22.